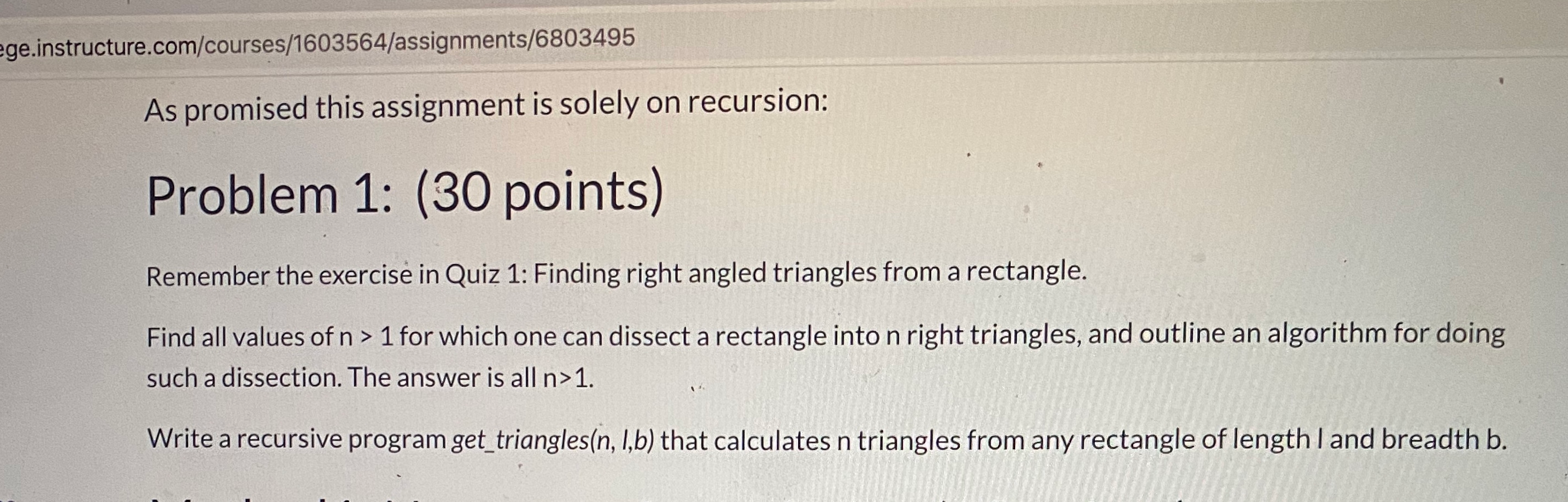
ge.instructure.com/courses/1603564/assignments/6803495 As promised this assignment is solely on recursion: Problem 1: (30 points) Remember the exercise in Quiz 1: Finding right angled triangles from a rectangle. Find all values of n > 1 for which one can dissect a rectangle into n right triangles, and outline an algorithm for doing such a dissection. The answer is all n>1. Write a recursive program get_triangles(n, 1,b) that calculates n triangles from any rectangle of length I and breadth b. s Method1: Non recursive solution (10 points) If I call get_triangles(4,8,5): It could return rdings "4 triangles: base: 5, height 4" or "..... base: 4, height 5" ces serves However, if I call triangles(5, 8, 5): It should return "3 triangles, base: 5, height 4" or "3 triangles base: 4, height 5" "1 triangle base: 3.125, height 2.49" "1 triangle: base: 3.125, height 3.9" In the example I mentioned, if n is even, I am dividing the rectangle into n/2 rectangles and then dividing each rectangle into two if nis odd, I am dividing the rectangle into (n-1)/2 rectangles and then dividing each rectangle into two and one resulting triangle into half. Make sure you can run this by hand before coding it Method2: recursive (20 points) First divide the rectangle into 2 right triangles. Then recursively divide the triangles until you have reached n The first call creates 2 triangles: each subsequent call produces 1 extra triangle. Note: If you are unable to code this, I will accept an algorithm written in english for (5+10) points ge.instructure.com/courses/1603564/assignments/6803495 As promised this assignment is solely on recursion: Problem 1: (30 points) Remember the exercise in Quiz 1: Finding right angled triangles from a rectangle. Find all values of n > 1 for which one can dissect a rectangle into n right triangles, and outline an algorithm for doing such a dissection. The answer is all n>1. Write a recursive program get_triangles(n, 1,b) that calculates n triangles from any rectangle of length I and breadth b. s Method1: Non recursive solution (10 points) If I call get_triangles(4,8,5): It could return rdings "4 triangles: base: 5, height 4" or "..... base: 4, height 5" ces serves However, if I call triangles(5, 8, 5): It should return "3 triangles, base: 5, height 4" or "3 triangles base: 4, height 5" "1 triangle base: 3.125, height 2.49" "1 triangle: base: 3.125, height 3.9" In the example I mentioned, if n is even, I am dividing the rectangle into n/2 rectangles and then dividing each rectangle into two if nis odd, I am dividing the rectangle into (n-1)/2 rectangles and then dividing each rectangle into two and one resulting triangle into half. Make sure you can run this by hand before coding it Method2: recursive (20 points) First divide the rectangle into 2 right triangles. Then recursively divide the triangles until you have reached n The first call creates 2 triangles: each subsequent call produces 1 extra triangle. Note: If you are unable to code this, I will accept an algorithm written in english for (5+10) points