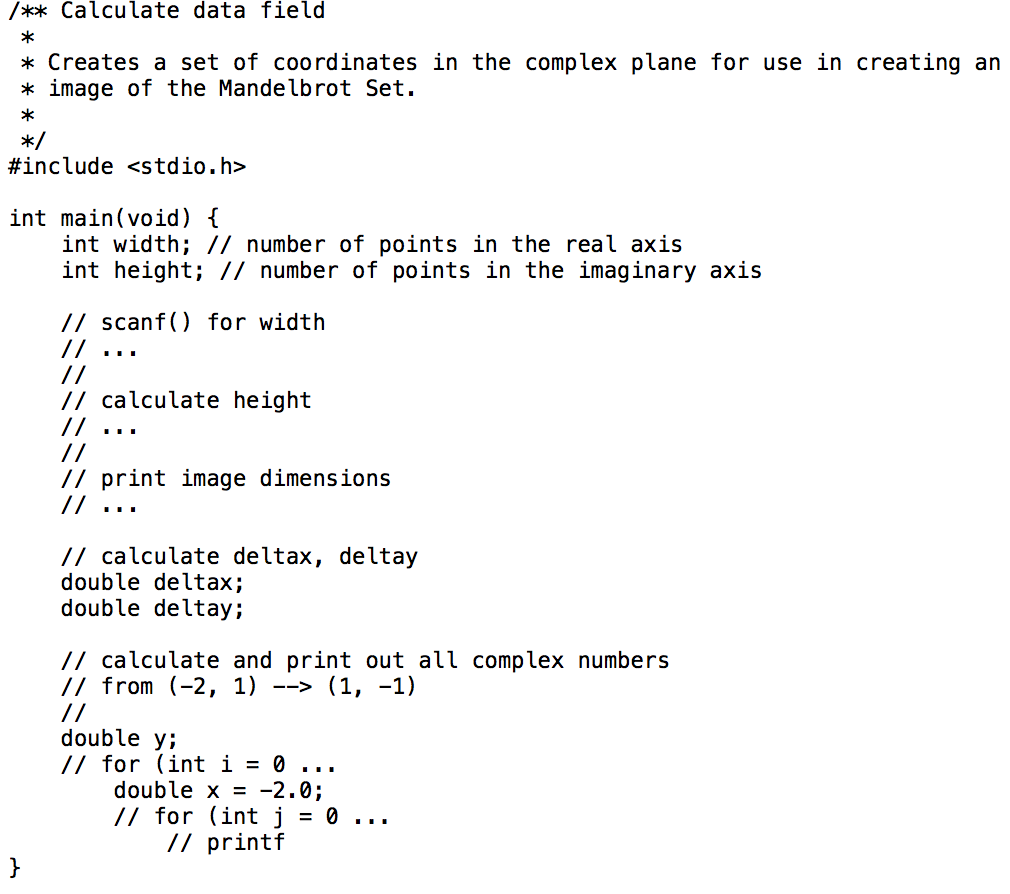
Generating complex numbers A complex number, in the form C-yi, consists of a real portion a, and an imaginary portion, yi. A complex number can be visualised as a pair of coordinates, (x, y), with the horizontal axis representing the real portion, and the vertical axis representing the imaginary portion The drawing in Figure 1 extends from -2, 1) in the top-left corner to 1) at the bottom right Consider that each pizel corresponds to a single compler number. If you wanted to draw a picture of the Mandelbrot set, and knew the size of the image (for example, 300 pixels wide by 200 pixels high), then you could calculate all of the complex numbers for all of the pixels. In your program, you will generate the complex co-ordinates, starting at the top- left corner, and proceeding row-by-row, until the last co ordinate is generated, corresponding to the bottom-right corner. This is shown in the matrix below: (-2+2ax,1) (1,1) -2,1-2Ay) (-2,-1) (-2 + ,1) Generating complex numbers A complex number, in the form C-yi, consists of a real portion a, and an imaginary portion, yi. A complex number can be visualised as a pair of coordinates, (x, y), with the horizontal axis representing the real portion, and the vertical axis representing the imaginary portion The drawing in Figure 1 extends from -2, 1) in the top-left corner to 1) at the bottom right Consider that each pizel corresponds to a single compler number. If you wanted to draw a picture of the Mandelbrot set, and knew the size of the image (for example, 300 pixels wide by 200 pixels high), then you could calculate all of the complex numbers for all of the pixels. In your program, you will generate the complex co-ordinates, starting at the top- left corner, and proceeding row-by-row, until the last co ordinate is generated, corresponding to the bottom-right corner. This is shown in the matrix below: (-2+2ax,1) (1,1) -2,1-2Ay) (-2,-1) (-2 + ,1)