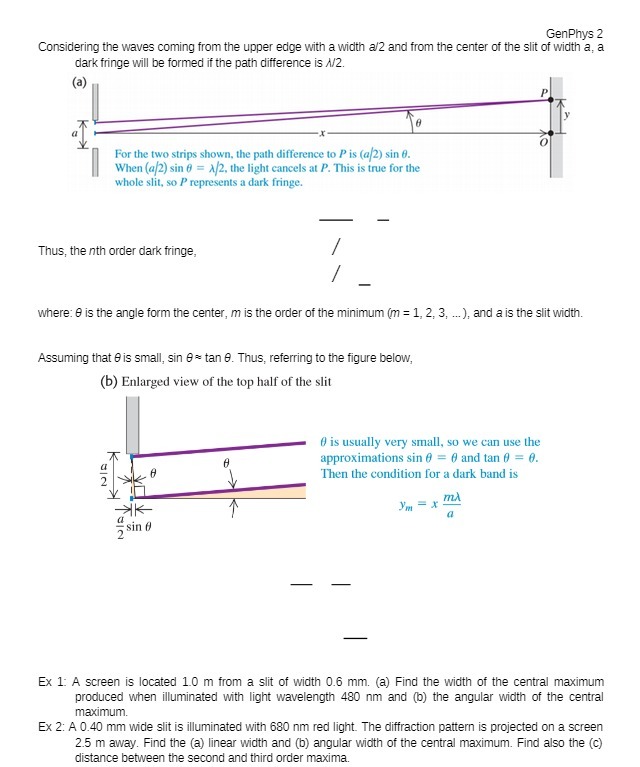
GenPhys 2 Considering the waves coming from the upper edge with a width a/2 and from the center of the slit of width a, a dark fringe will be formed if the path difference is A/2. (a) For the two strips shown, the path difference to P is (a/2) sin d. When (a/2) sin 0 = A/2, the light cancels at P. This is true for the whole slit, so P represents a dark fringe. Thus, the nth order dark fringe, where: 0 is the angle form the center, m is the order of the minimum (m = 1, 2, 3, ...), and a is the slit width. Assuming that 0 is small, sin 0 = tan 0. Thus, referring to the figure below, (b) Enlarged view of the top half of the slit # is usually very small, so we can use the approximations sin 0 = # and tan o = 0. Then the condition for a dark band is Ym= X MA a sin Ex 1: A screen is located 10 m from a slit of width 0.6 mm. (a) Find the width of the central maximum produced when illuminated with light wavelength 480 nm and (b) the angular width of the central maximum. Ex 2: A 0.40 mm wide slit is illuminated with 680 nm red light. The diffraction pattern is projected on a screen 2.5 m away. Find the (a) linear width and (b) angular width of the central maximum. Find also the (c) distance between the second and third order maxima