Give an example describing a queuing system using the Kendall-Lee notation (like M/M/s).

Give an example of applying Little's law to a queuing system problem.

Define and give an example of a stochastic process

Define and give an example of discrete vs. continuous time stochastic processes

Define and give and example of discrete vs. continuous state space stochastic processes.

Define what is meant when a stochastic process is Markovian

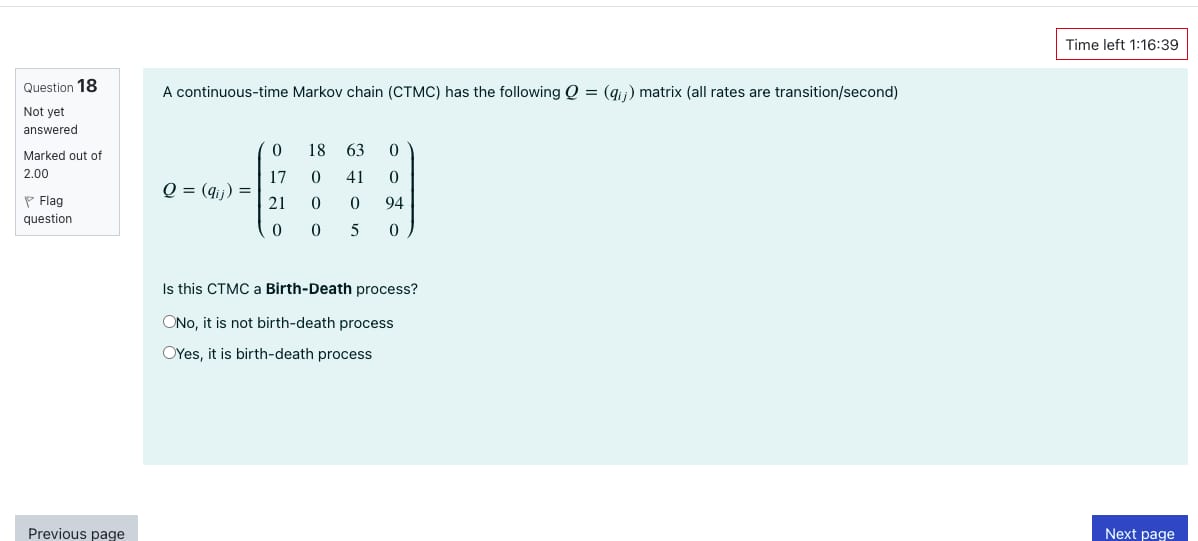
Time left 1:16:39 Question 18 A continuous-time Markov chain (CTMC) has the following O = (q, ) matrix (all rates are transition/second) Not yet answered Marked out of 0 18 63 0 2.00 17 0 41 0 0 = (q)) = Flag 21 0 0 94 question 0 0 5 0 Is this CTMC a Birth-Death process? ONo, it is not birth-death process OYes, it is birth-death process Previous page Next pageQuestion 3 1 pts Which of the following statements is FALSE about regression analysis? O Regression analysis falls under predictive analytics. O We use regression analysis to understand the distribution of a variable O We use the regression analysis to assess the relationship between dependent and independent variables. We use the regression analysis to explain the change in dependent variable as a result of change in independent variables.Q. 6 In this problem we deal with Bivariate Gaussians. Please read the lecture notes available under the 'Bivariate Gaussian RVs' section on Canvas (L16.pdf). The lecture notes summarizes the following facts about bivariate Gaussians: X and Y are bivariate Gaussian if their joint PDF is given by HX - HX fx,y (x, y ) = 2noxGY (1 - Pxy ) 1/2 exp 2(1 -PxY) - 2PxY Ox Ox This PDF is specified by 5 parameters which correspond to the marginal means, variances and correlation, i.e., (X, Y) ~ N(ux, MY, ox, 67, pxY). Some interesting facts about bivariate Gaussians are listed below: . Marginals are Gaussian: X ~ N(ux, Gx ) and X ~ N(ux, 63). . Bivariate Gaussian RVs are uncorrelated iff they are independent: If pyy = 0 then the joint density can be written as fx, y (x,y) = fx(x) fr ())= 2nox -e- ( x- ux )/20% 1 - ()-MY)2 /20% V2noy thus the RVs are independent. . A linear transformation of bivariate Gaussian is also bivariate Gaussian, but with new parameters. . Bivariate Gaussian and conditioning: For bivariate Gaussian RVs (X, Y) the conditional distributions fry and frix are also Gaussian, and are given by, frix (y | x) = fxr (x, y) - exp (y - HYLx (x))2) fx (x) V2noylx 20 yx ~ N( ur x, 0; x ), where E[Y [ X] = Myx (X) = Hy + Pxy ox (X -ux ) and Gyx = of (1 - Pxy). Suppose that X ~ N(0, 1) and Y ~ N(1, 2) are two independent Gaussian random variables. Define random variables U and V as U = X + Y, V = X + ay for some a. 1. What is the joint distribution of U, V in terms of o? 2. Find o (if it exists) such that U and V be independent. 3. Find the conditional distribution fulv (u|5)