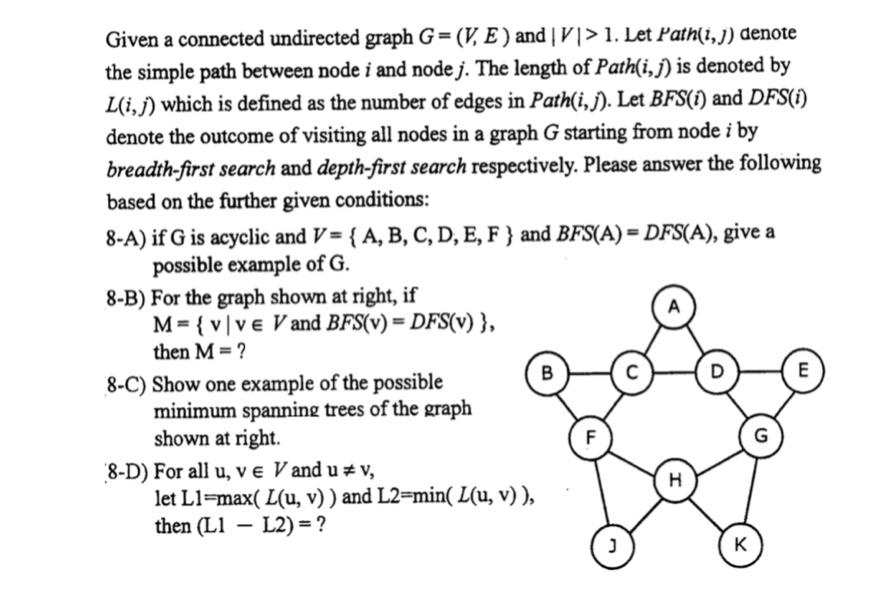
Given a connected undirected graph G=(V, E) and IVI>1. Let Path(i,y) denote the simple path between node i and node j. The length of Path(i,j) is denoted by L(i,j) which is defined as the number of edges in Path(i,j). Let BFS(i) and DFS(i) denote the outcome of visiting all nodes in a graph G starting from node i by breadth-first search and depth-first search respectively. Please answer the following based on the further given conditions: 8-A) if G is acyclic and V = {A, B, C, D, E, F } and BFS(A) = DFS(A), give a possible example of G. 8-B) For the graph shown at right, if A M= { vlve V and BFS(v) = DFS(v) }, then M = ? 8-C) Show one example of the possible B E minimum spanning trees of the graph shown at right. F G 8-D) For all u, ve V and u = V, H let Ll=max( L(u, v)) and L2=min( L(u, v)), then (L1 - L2) =