Given a function:

f$($x$)=$ x$^4-7\mathrm{.}2$x$^3+15\mathrm{.}8$x $-1\mathrm{.}9$

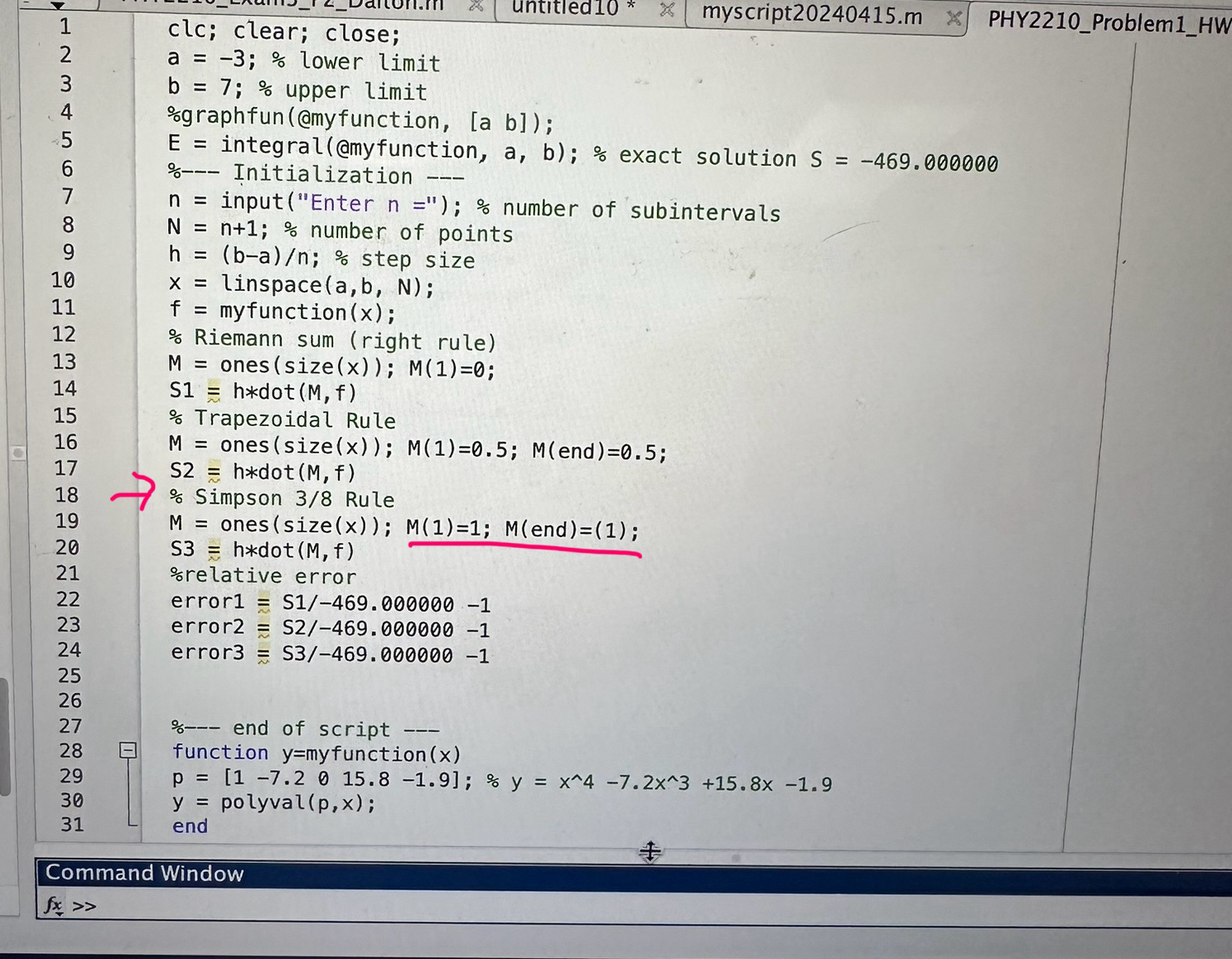
Calculate numerically the integral value of the function within the interval $[-3,7].$ Your method must have variable number of sub intervals n$.$ Your script must include the following line

n $=$input$("$Enter n$=")$;

The exact value of the integral is $-469\mathrm{.}000000.$ Use three different methods:

a$.)$ Riemann sum right rule

b$.)$ Trapezoidal rule

c$.)$ Simpsons method $3/8$ rule.

d$.)$ calculate relative error for each method

$($error $=$ calculated$/$ exact $-1)$;

Is my MATLAB code right? What is supposed to be the M$(1)$ and M$($end$)$ value for Simpsons $3/8$ rule? I am getting an incorrect value for Simpsons rule.

The command window gives me:

S$1=-483\mathrm{.}0743$

S$2=-467\mathrm{.}5743$

S$3=-445\mathrm{.}3910$

Error$1=0\mathrm{.}0300$

Error$2=-0\mathrm{.}0030$

Error$3=-0\mathrm{.}0503$

S$3$ must be closest to $-469$ and error$3$ must be the smallest, but it's not. Therefore it's incorrect. What should my M values be changed to$?$