Given a m * n matrix, your task is to compute a path from any element on the 1st column to any element on the last column at minimal cost. The path consists of several steps, each step is moving from column j to column j+1 in an adjacent (horizontal or diagonal) row. The first row and the last row are considered as adjacent rows. The cost of a path is the sum of visited integers.

The two slightly different matrices are shown in figure below. The minimum cost path is illustrated in the figure and the 2nd path takes advantage of the adjacency property of the first and last row.

You'll be given two integers m and n that indicate the number of rows and columns at the first line. The next m lines will be the matrix and each line represents one row of the given matrix. You're required to output the minimum cost.

Notes: The test cases have the properties: number of rows is between 1 and 10; number of columns is between 1 and 100; number in matrix can be positive or negative; All path weights can be represented by 30-bit signed integer.

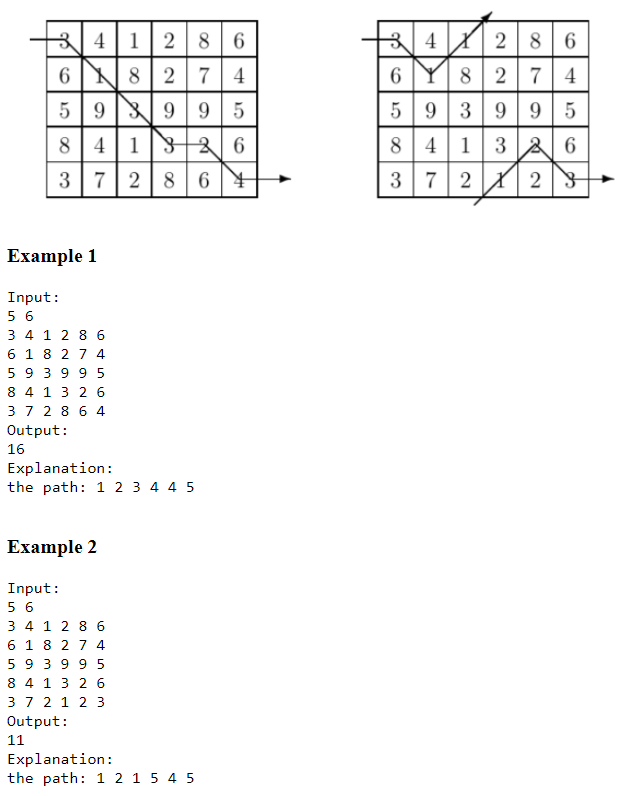
34 128 6 6 N827 4 5999 5 84 1126 3 | 7 286 34 x 286 6Y|827 274 5 9 3 9 9 5 8 41 326 3 7 2 x 25 Example 1 Input: 5 6 3 4 1 286 6 1 8 2 74 5 9 3 9 9 5 8 4 1 3 2 6 3 7 2 8 64 Output: 16 Explanation: the path: 1 2 3 4 4 5 Example 2 Input: 5 6 3 4 1 2 86 6 1 8 2 7 4 5 9 3 9 9 5 8 4 1 3 2 6 3 7 2 1 2 3 Output: 11 Explanation: the path: 1 2 1 5 4 5 34 128 6 6 N827 4 5999 5 84 1126 3 | 7 286 34 x 286 6Y|827 274 5 9 3 9 9 5 8 41 326 3 7 2 x 25 Example 1 Input: 5 6 3 4 1 286 6 1 8 2 74 5 9 3 9 9 5 8 4 1 3 2 6 3 7 2 8 64 Output: 16 Explanation: the path: 1 2 3 4 4 5 Example 2 Input: 5 6 3 4 1 2 86 6 1 8 2 7 4 5 9 3 9 9 5 8 4 1 3 2 6 3 7 2 1 2 3 Output: 11 Explanation: the path: 1 2 1 5 4 5