Given a set P of n points in R^

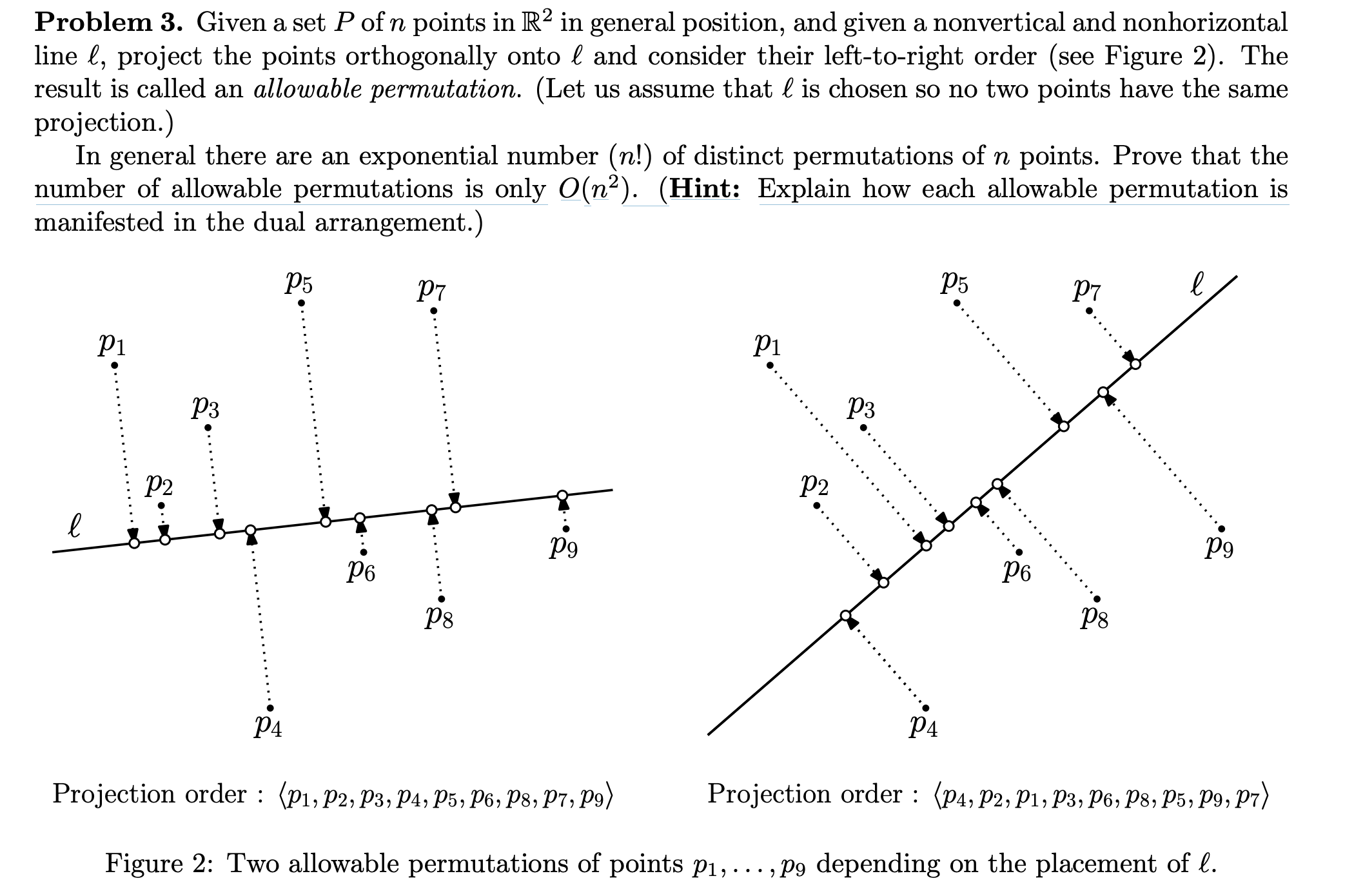
Problem 3. Given a set P of n points in R2 in general position, and given a nonvertical and nonhorizontal line E, project the points orthogonally onto 6 and consider their left-to-right order (see Figure 2). The result is called an allowable permutation. (Let us assume that E is chosen so no two points have the same projection.) In general there are an exponential number (n!) of distinct permutations of n points. Prove that the number of allowable permutations is only Q0112). (Hint: Explain how each allowable permutation is manifested in the dual arrangement.) p5 P7 p5 P7 6 .o P4 Projection order : (p17p21p37p4>p5>p63p81p7>p9> Projection order 2 (p47p27p17p3ap51p8>p5>p97p7) Figure 2: Two allowable permutations of points In, . . . , p9 depending on the placement of .6