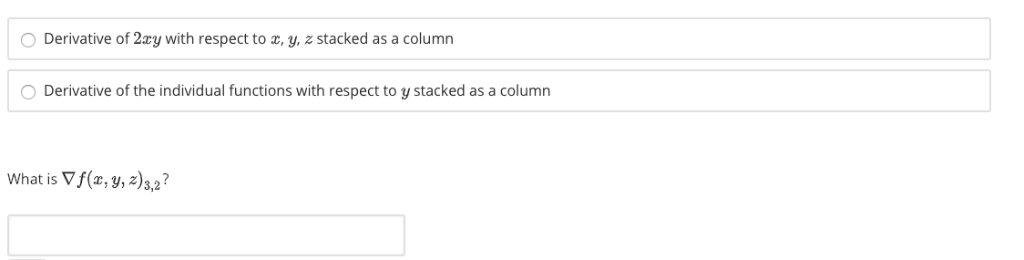
Given a vector-valued function f: Rd R, the gradient or the gradient matrix of f, denoted by Vf, is the d x k matrix - (+48) Vf Vf2 Vf Let f (x, y, z) af ????1 How many columns does Vf (x, y, z) have? 8f d This is also the transpose of what is known as the Jacobian matrix Jf of f. x +z+z C 2xy y +2 How many rows does Vf (x, y, z) have? What does column 2 represent in the gradient matrix? afle da : afk td O Derivative of 2xy with respect to x, y, z stacked as a column O Derivative of the individual functions with respect to y stacked as a column What is Vf(x, y, z) 3,2?