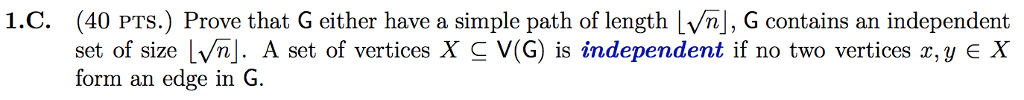
Given an undirected graph G with n vertices, the greedy coloring algorithm order the vertices of G in an arbitrary order vi,... , vn Initially all the vertices are not colored. In the ith iteration, the algorithm assigns Vi the smallest color (i.e., positive integer) k such that none of its neighbors that are already colored have color k. Let f(vi) denote the assigned color to vi. (40 PTS.) Prove that G either have a simple path of length lvnj, G contains an independent set of size Lvhj. A set of vertices X-V(G) is independent if no two vertices z, y E X form an edge in G. 1.C