Given are n interpolation points (x_i , f_i), i = 0, 1, . . . , n, where for all i not= j: x_i not= x_j . The Lagrange interpolating polynomial has the form

p(x) = l 0(x)f0 + l 1(x)f(x1) + + l n(x)fn, where

l_i(x_j) = 1 if i = j , 0 if i not= j

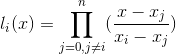
In this form, we have that p(xi) = fi , i = 0, 1, . . . , n.

Write a pseudo description for the computation of p(x). Prove that the algorithm to compute p(x) runs in O(n^2 ) time.