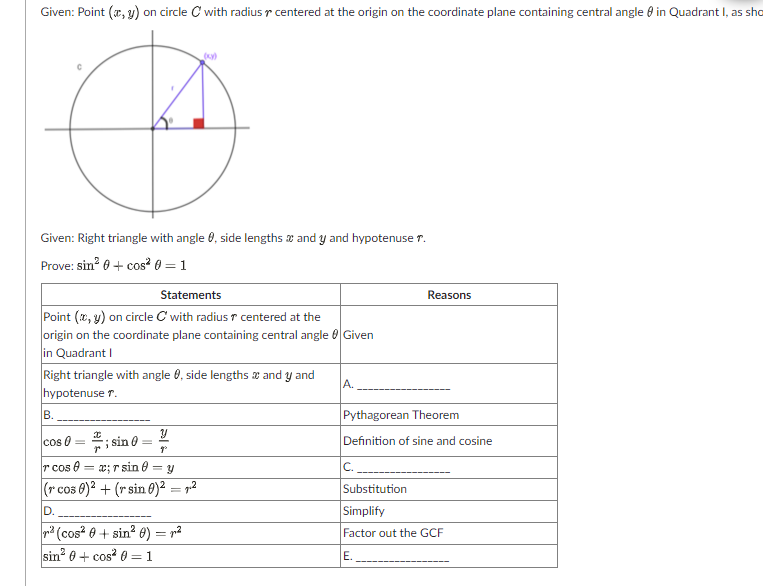
Question: Given: Point (@, y) on circle C with radius ~ centered at the origin on the coordinate plane containing central angle / in Quadrant I,
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


