Given that:

2) Now you will plan for your retirement. To do this we need to first determine a couple of values.

a. How much will you invest each year? Even $25 a month is a start ($300 a year), youll be surprised at how much it will earn. You can choose a number you think you can afford on your life circumstances or you can dream big. State what you will use for P, r, and n to earn credit.

1. P= $300 each year

r= 8% compounded annually

n= 1

b. Determine the formula for the accumulated amount that you will have saved for retirement as a function of time and be sure to simplify it as much as possible. You need to be able to show me what you used for r, n, and P so that I can calculate your answers. Plug in those values into the formula and simplify the equation.

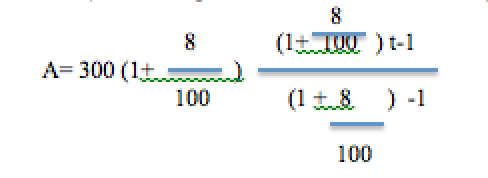
A=4050 [( 1.08)^ t-1]

d) When do you want to retire? Use this to determine how many years you will be investing.(65 years old is a good retirement-age estimate). You need to say how old you are if you are retiring when you are 65 or tell me how long until you retire. State what you will use for t.

I want to retire at 65, and I am investing at the age of 25 years. Because of this, t=(65-25) years =40 years.

e) Determine how much you will have at retirement using the values you decided upon above.

The amount I will have at retirement is = $ [4050* (1.08^40 -1)] = $83934.31

f) How much of that is interest?

The interest amount would be = $[83934.31- (40*300)]= $71934.31

g. Now lets say you wait just 5 years before you start saving for retirement, how much will that cost you in interest? How about 10 years? How about just 1 year?

If we wait just 5 years before we start saving for retirement, then the decreased interest amount is

= [4050(1.08⁴⁰-1.08³⁵)-(5*300)] = 26603.67

If we wait just 10 years before we start saving for retirement, then the decreased interest amount is

= [4050(1.08⁴⁰-1.08³⁰)-(10*300)] = 44230.55

If we wait just 1 years before we start saving for retirement, then the decreased interest amount is

= [4050(1.08⁴⁰-1.08³⁹)-(1*300)] = 6217.36

h. Determine how much you will have to live on each year. Note, we are neither taking into account taxes nor inflation (which is about 2% a year).

The required amount is = [4050(1.08⁴⁰-1)/25] = 3357.37

Therefore, 3357.37 will be available for each year.

i. How much would you need to have accumulated before retirement?

The required amount is = (25*50000) = 1250000

Therefore, we need $1250000 to have accumulated before retirement

j. How much would you need to start investing each year, beginning right now, to accumulate this amount? A short-cut to doing this is to first compute the effective yield at your retirement age, then divide this amount into Part (i). This is the amount you well need to invest each year.

Let P be the amount that will be invested every year before retirement

Then,

12.5*P[1.08⁴⁰-1] = 1250000

P[1.08⁴⁰-1] = 1250000/12.5

P[1.08⁴⁰-1] = 100000

P = 100000/[1.08⁴⁰-1]

P = 4825.21

Therefore, we need 4825.21 to start investing each year, beginning right now, to accumulate the amount 1250000 before retirement.

FIND K.

k. That was just using $35,000, how much would you want to have each year to live on? Dream big or reasonable depending on your occupation! Now using that value, repeat parts (i) and (j) again. You need to state what you would want to live on and it needs to be something besides $35,000.

8 (1+ 10 ) t-1 8 A=300 (1+ 100 (1 + 8 ) -1 100