Question: Given the autonomous differential equation: d y d t = 0 . 2 y ( 5 - y ) ( y - 2 ) a
Given the autonomous differential equation:
a Find the equilibrium points. Classify each of them as stable, unstable, or semistable.
b Sketch a graph of vs in the ytplane. Draw several solution curves.
c Suppose that this equation models a population of rats given in thousands of rats for a particular region. Explain the meaning of and in the model. What do they represent?
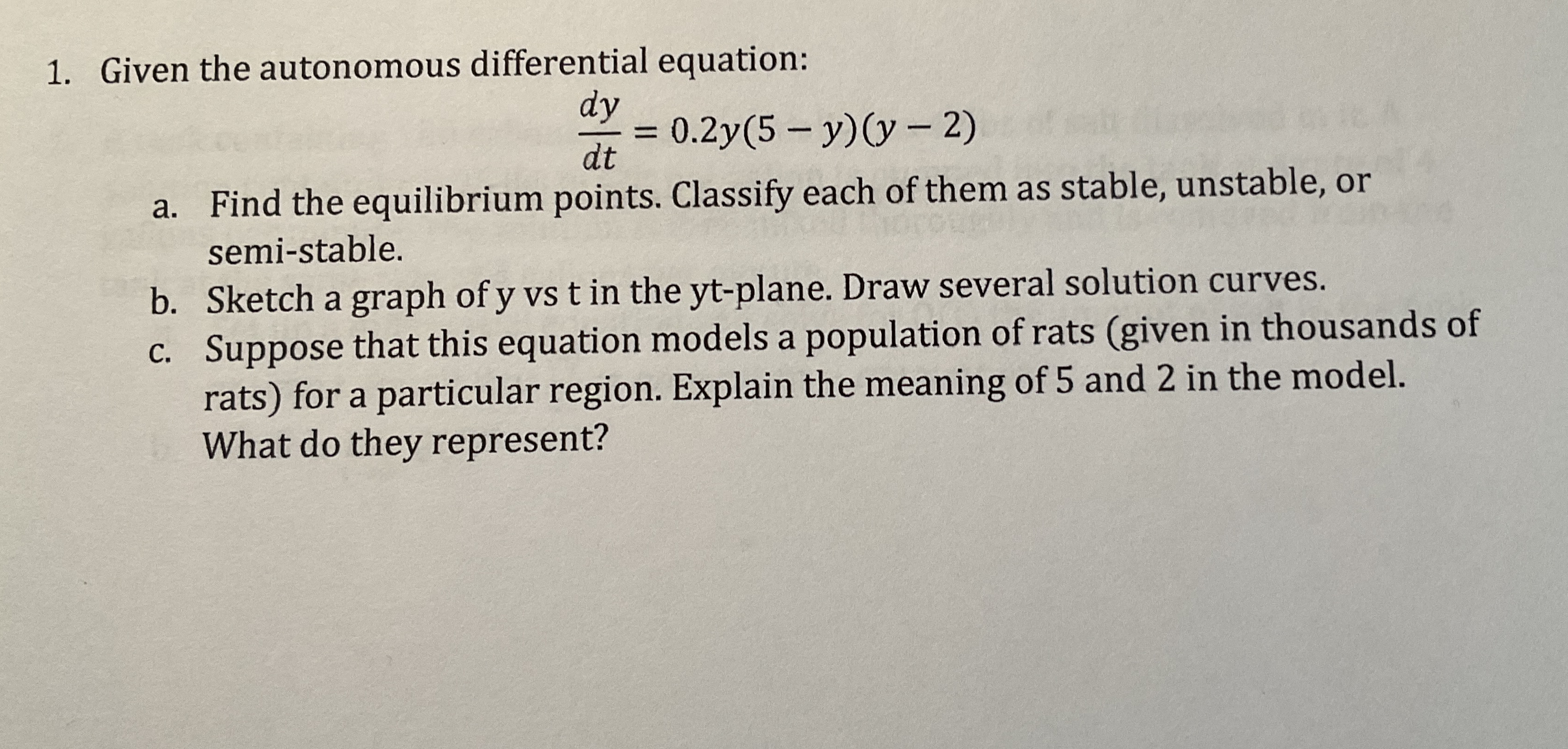
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


