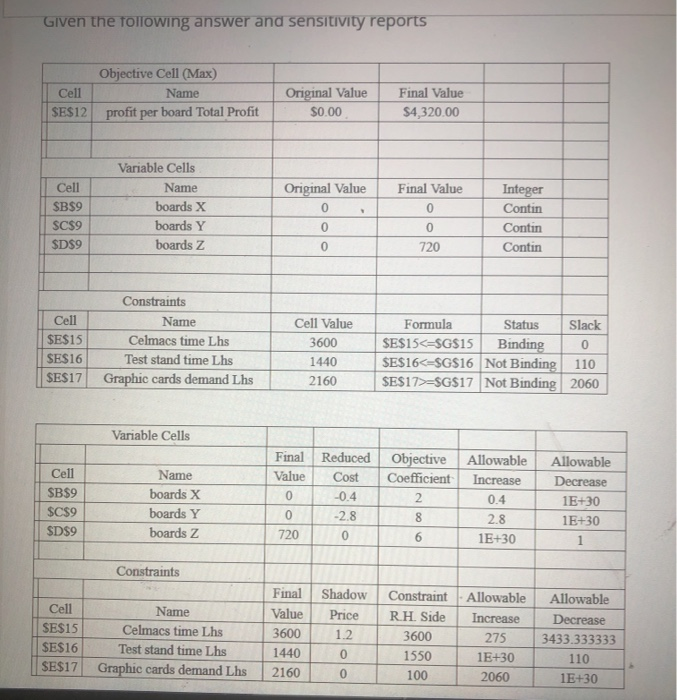
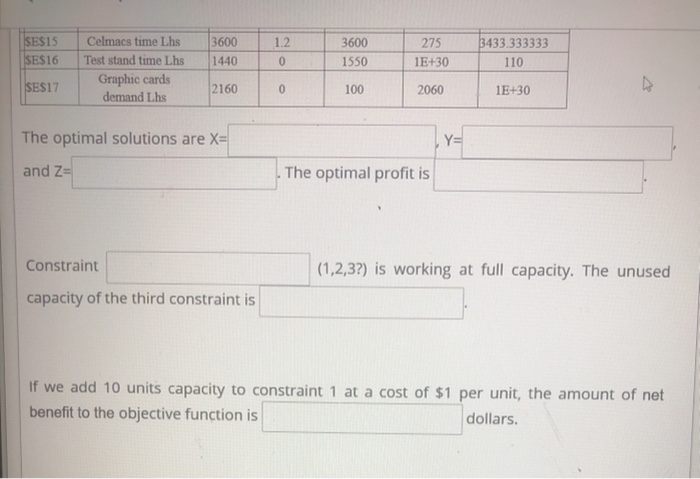
Question: Given the following answer and sensitivity reports Cell SE$12 Objective Cell (Max) Name profit per board Total Profit Original Value $0.00 Final Value $4,320.00 Variable

Given the following answer and sensitivity reports Cell SE$12 Objective Cell (Max) Name profit per board Total Profit Original Value $0.00 Final Value $4,320.00 Variable Cells Name boards X boards Y boards z Original Value 0 Cell SB$9 SC$9 $D$9 1 Final Value 0 0 720 Integer Contin Contin Contin 0 0 Cell $E$15 SES16 $E$17 Constraints Name Celmacs time Lhs Test stand time Lhs Graphic cards demand Lhs Cell Value 3600 1440 2160 Formula Status Slack $E$15=SG$17 Not Binding 2060 Variable Cells Objective Coefficient 2 Cell $B$9 $C$9 SD$9 Final Reduced Value Cost 0 -0.4 0 -2.8 720 0 Name boards X boards Y boards z Allowable Increase 0.4 2.8 1E+30 Allowable Decrease 1E+30 1E+30 8 6 Constraints Cell SE$15 $E$16 $E$17 Name Celmacs time Lhs Test stand time Lhs Graphic cards demand Lhs Final Value 3600 1440 2160 Shadow Price 1.2 0 Constraint Allowable RH. Side Increase 3600 275 1550 1E+30 100 2060 Allowable Decrease 3433.333333 110 1E+30 0 3600 275 SES15 SES16 1.2 0 3600 1550 3433.333333 110 1440 1E+30 Celmacs time Lhs Test stand time Lhs Graphic cards demand Lhs SES17 2160 0 100 2060 1E+30 The optimal solutions are X= Y= and Z= The optimal profit is Constraint (1,2,3?) is working at full capacity. The unused capacity of the third constraint is If we add 10 units capacity to constraint 1 at a cost of $1 per unit, the amount of net benefit to the objective function is dollars

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

Cell SE$12 Objective Cell (Max) Name profit per board Total Profit Original Value $0.00 Final Value $4,320.00 Final Value Variable Cells Name boards X boards Y boards Z Cell SB$9 $C$9 $D$9 Original...

For a product mix linear programming problem, we use three materials (A, B and C) to make two products (X and Y) to maximize total profit. The following screenshot are the Answer and Sensitivity...

Please see Exhibit C in the file named "Exhibit C.pdf" posted on iLearn. Based on the data in Exhibit C, What are the optimal quantities of product 1, 2 and 3 to produce? Select one: a. 0, 4, 48 b....

Please see Exhibit C in the file named "Exhibit C.pdf" posted on iLearn. Based on the data in Exhibit C, How many hours of labor are left unused when producing the optimal quantities of product 1, 2,...

Exhibit C A manufacturer plans to make three types of product next year. The profits per unit of product 1, 2 and 3 are $12, S18 and $15 respectively. The process requires machine time, labor hours...

Exhibit C A manufacturer plans to make three types of product next year. The profits per unit of product 1, 2 and 3 are $12, $18 and $15 respectively. The process requires machine time, labor hours...

Please see Exhibit C in the file named "Exhibit C.pdf" posted on iLearn. Based on the data in Exhibit C, which resource(s) is (are) used up? Select one: a. Machine time and Labor hours b. Materials...

Please see Exhibit C in the file named "Exhibit C.pdf" posted on iLearn. Based on the data in Exhibit C, Which resource (s) is (are) not used up? Select one: a. Machine time and Materials O b....

We are taking off! A new airline company Jump! has sprung up in Australia, specialising in charter flights between Adelaide and Kangaroo Island. There has been a huge demand from travellers,...

If the surface of a cone of slant height C and base radius r is cut along a lateral edge and laid flat, it becomes the sector of a circle of radius C and central angle Î¸ (see Figure 19)....

How is the $36 per DLH MOH allocation rate computed? manufacturing overhead costs (MOH) are allocated using direct labor hours (DLLs) Total MOH cost = 936,000,000 Quantity 1000,000 units unit costs:...

You just bought a new luxury sports car for $ 1 3 1 , 0 0 0 . Before you had time to get insurance, the car was wrecked. Weird Wally offers to take it off your hands for $ 1 0 . 0 0 0 . You can then...

A congenital anomaly is present at or existing from the time of birth. True False QUESTION 2 The first chapter in ICD-10-CM is titled Diseases of the Circulatory System. True False QUESTION 3 NEC...