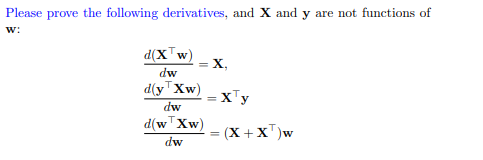
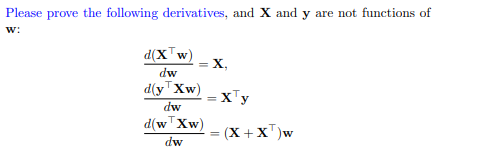
Given the following denominator layout derivatives, (2 points) . Differentiation of a scalar function w.r.t. a vector: If f(w) is a scalar function of d variables, w is a d x 1 vector, then differentiation of f(w) w.r.t. w results in a d x 1 vector of df ( w) dw wod . Differentiation of a vector function w.r.t. a vector: If f(w) is a vector function of size h x1 and w is a dx 1 vector, then differentiation of f(w) w.r.t. w results in a d x h vector afi afh df (w) = dw afh ThedPlease prove the following derivatives, and X and y are not functions of d(X w) - X, dw d(y Xw) = X V dw d(w Xw) = (X+X )w dw