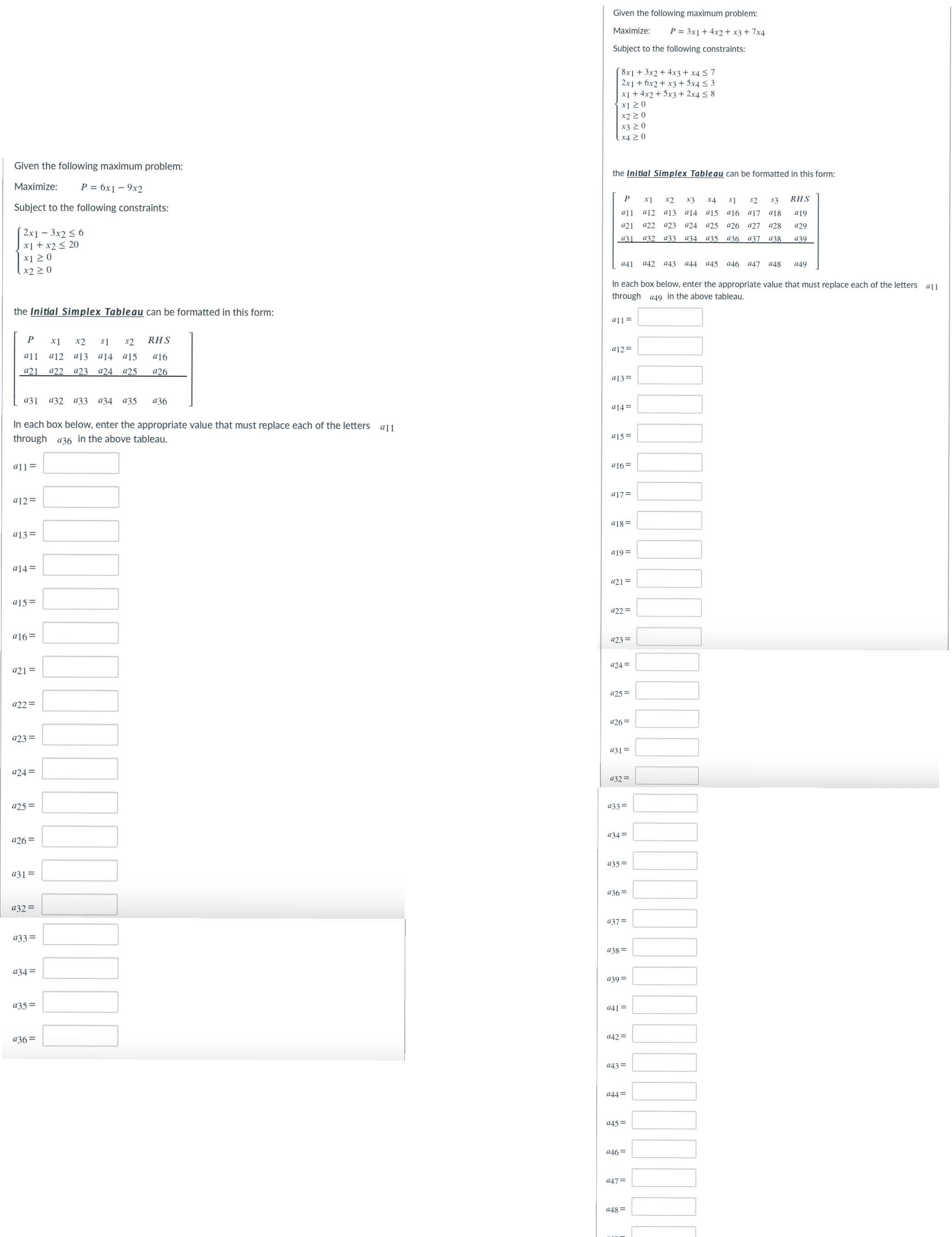
Given the following maximum problem: Maximize: P = 3x1 + 4x2+ x3 + 7x4 Subject to the following constraints: 8x1 + 3x2 + 4x3 + x4 57 2x1 + 6x2+x3+ 5x4 5 3 x1 + 4x2 + 5x3+ 2x4 5 8 x1 2 0 X3 20 x4 20 Given the following maximum problem: the Initial Simplex Tableau can be formatted in this form: Maximize: P = 6x1 - 9x2 P x1 x2 x3 x4 s $2 53 RHS Subject to the following constraints: a11 a12 13 a14 a15 a16 a17 a18 a19 a21 a22 a23 a24 425 a26 a27 a28 429 2x1 - 3x2 S 431 432 433 434 439 x1 + x2 5 20 x120 a41 042 043 44 045 046 047 948 949 x2 20 In each box below, enter the appropriate value that must replace each of the letters all through a49 in the above tableau. the Initial Simplex Tableau can be formatted in this form: 011= P x1 x2 $1 $2 RHS a 12= all a12 a13 a14 15 a16 a21 a22 a23 a24 a25 426 413= a31 432 433 a34 435 a36 014 = In each box below, enter the appropriate value that must replace each of the letters all through a36 in the above tableau. @15= 416= 417= a 12 = @18 = a13= a19= a14 = 421 = a15 = a22 = a16= 423= 424 = 421 = a25 = a22 = 426= a23 = 431 = a24 = a32 = 425 = 433 = a26 = 434 = a35= 431 = 436 = a32 = 437 = 433 = 438 = a34 = 439 = 435 = 041 = a36 = Q42 = Q43 = Q44 = 045= 046= 047= a48 =