6. Given the project network and time (in days) and cost information listed below, what is the lowest possible cost after expediting the project by 3 days? (CBC = Cannot be crashed.

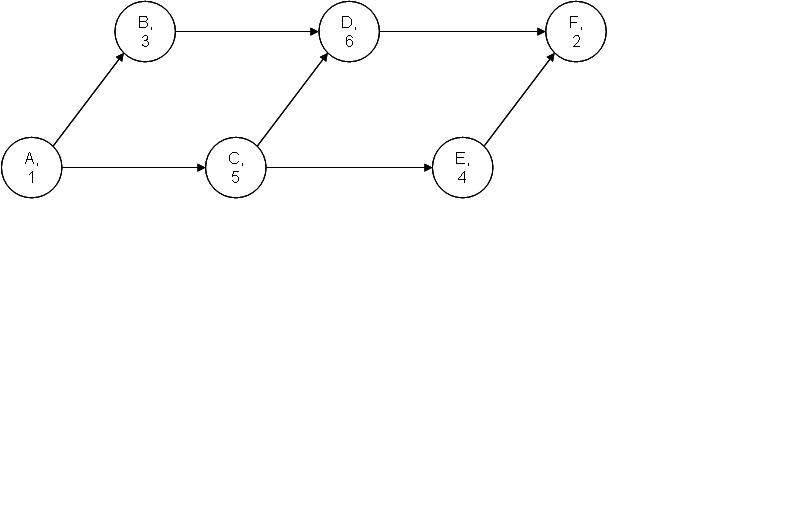
Activity	Normal Time	Crash Time	Normal Cost	Crash Cost
A	1	CBC	$400	CBC
B	3	2	$600	$700
C	5	2	$300	$1200
D	6	4	$200	$1000
E	4	2	$500	$800
F	2	1	$600	$800

A. $2900 B. $3100 C. $3300 D. $3400 E. $3600

7. In a G/G/1 queue, the average arrival rate is 10 customers per hour and the standard deviation of inter-arrival times is 12 minutes. The service time is 3 minutes per customer and its standard deviation is zero. The average queue length is:

A. 1/3 B. 1/2 C. 1 D. 2 E. None of the above

6. Consider a process consisting of two activities with different unit loads shown below (s for second):

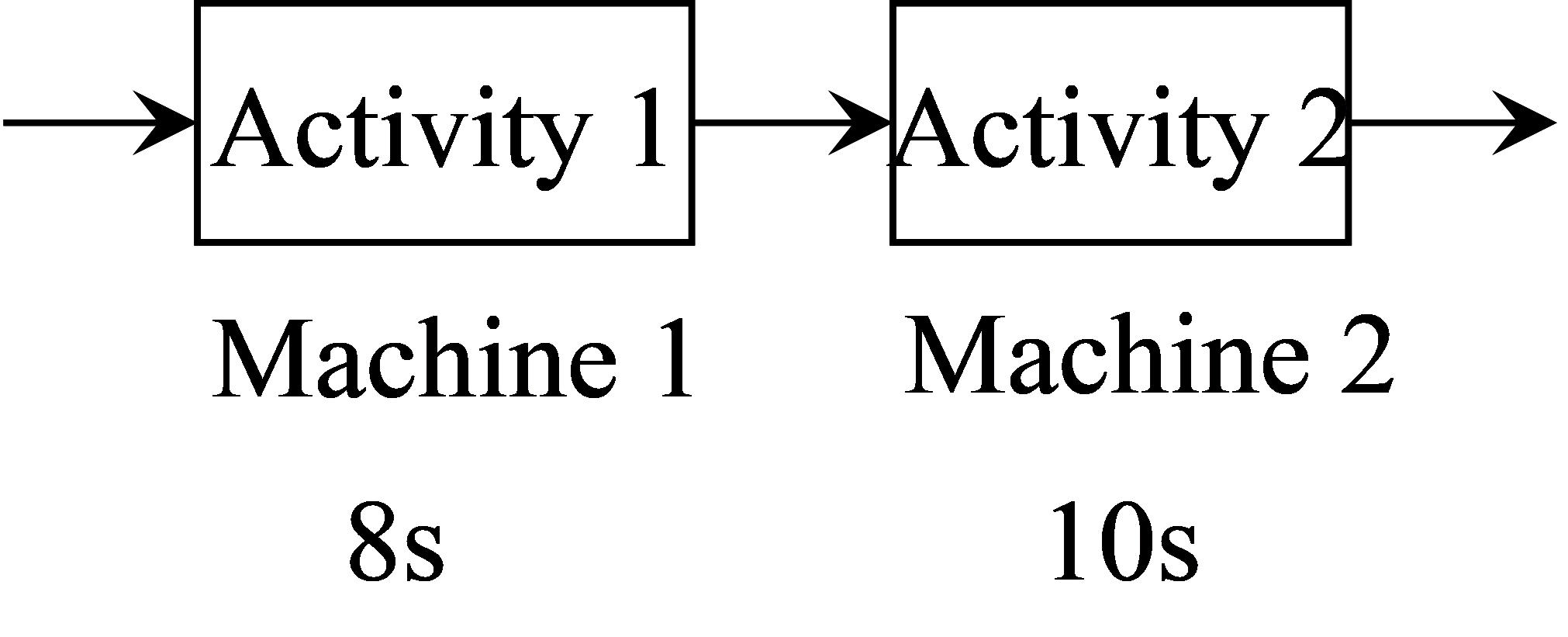
To double the output per hour, you can

A. Buy one more Machine 1 for Activity 1 (working in parallel)

B. Replace Machine 2 with a faster machine which cuts the unit load by half

C. Buy one more Machine 2 for Activity 2 (working in parallel)

D. Both B and C; E. None of the above

AT > Activity 1 Machine 1 >Activity 2 Machine 2 10s 85