Given the solution to the below :

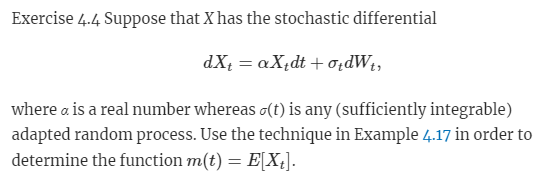
Example 4.17 Compute Elew. ]. Solution: Define Z by Z(t) = e*W. . The Ito formula gives us dZ(t) = hole"Widt + aeidWt, so we see that Z satisfies the stochastic differential equation (SDE) d71 = ha Zedt + aZ,dW., Zo = 1. In integral form this reads Zt = 1+502 Taking expected values will make the stochastic integral vanish. After moving the expectation within the integral sign in the ds-integral and defining m by me = E[Z.] we obtain the equation me = 1+ m,s. oExercise 4.4 Suppose that X has the stochastic differential dXt = axedt + oldWt, where a is a real number whereas o(t) is any (sufficiently integrable) adapted random process. Use the technique in Example 4.17 in order to determine the function m(t) = EX:]