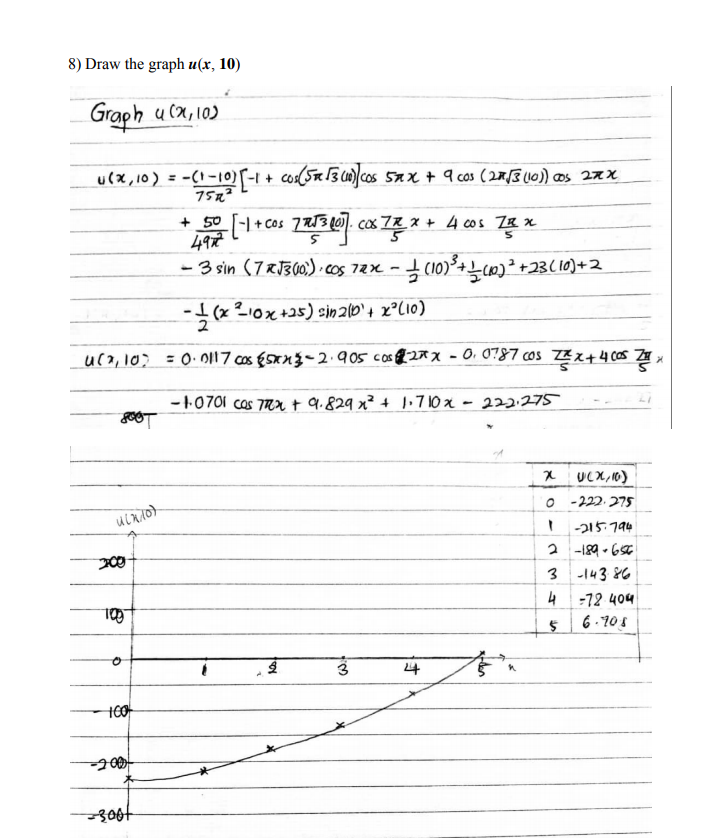
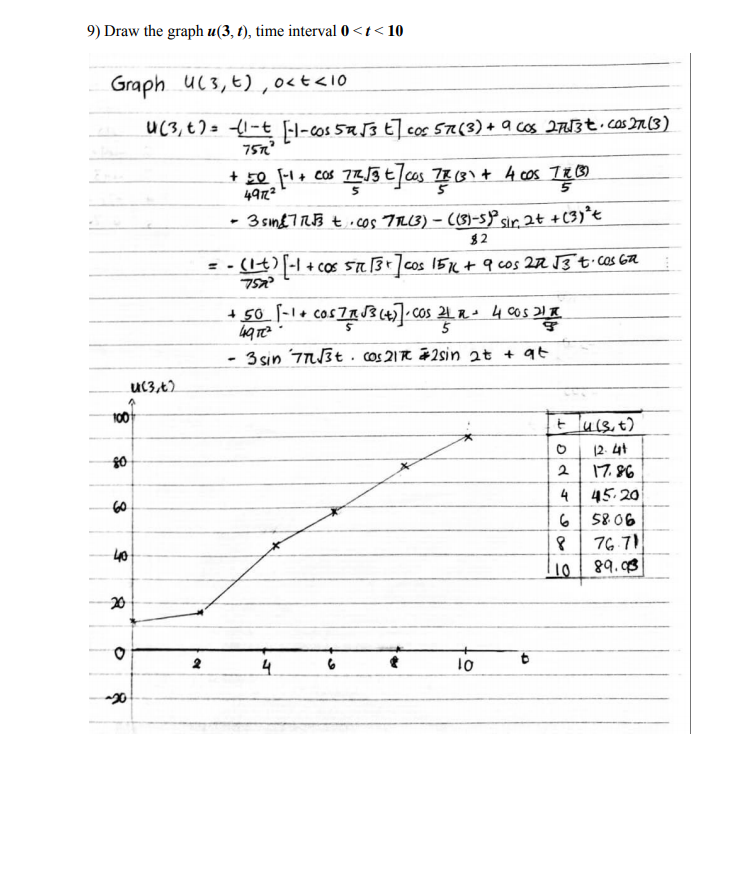
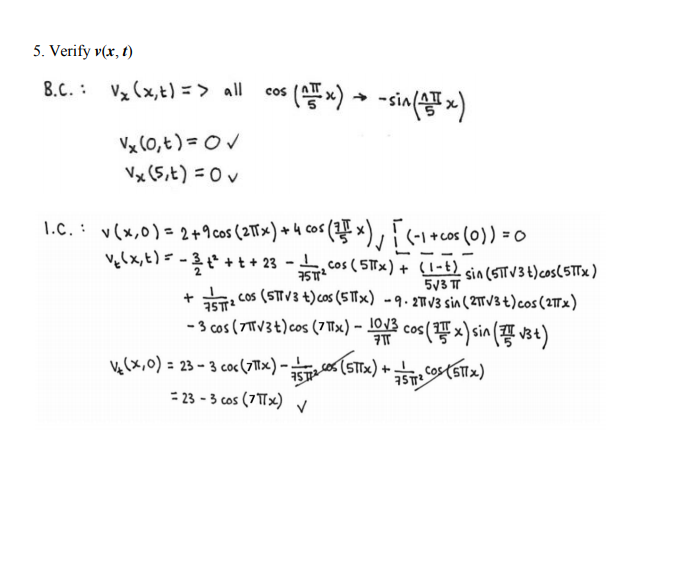Question: Given the string vibration problem as follows: . Length of the string is equal 5, tension is 12 and dense is equal 4. . On
Given the string vibration problem as follows: . Length of the string is equal 5, tension is 12 and dense is equal 4. . On the left hand end of the string it is given a force equal 5sin2/ and on the right hand end of the string it is given a force equal 10t. At initial form of the string is given as 9cos2Tx - 4cos (7:x / 5) + 2 At initial speed is equal -3cos 7xx + 10x - 2 . . There is a force acting on the string expressed by the function (1 - t)cos5xx - 6cos (7six/ 5) -3(2t - sin21) + 2(x - 5) 2sin2t - 3t + 1 Your task followings: 1. Specify the problem as mathematical model. Problem for u(x, (). 2. Write appropriate Transformation v(x, () for the Step 1. 3. Finalize Step 1 and specify the problem for v(x, (). 4. Find v(x, (). 5. Verify v(x, t) (means check if obtained solution v(x, f) satisfying all the conditions of the problem for the function v(x, ()). 6. Find the solution of the problem u(x, (). 7. Verify u(x, () (means check if obtained solution u(x, ()satisfying all the conditions of the problem for the function u(x, ()) 8. Draw the graph u(x, 10) which is the displacement of the string at the time f = 10. 9. Draw the graph u(3, () which is the displacement of the point x = 3 in the time interval 0 in 24) +2(x-5)kin 2+ -3t + 1 = 3Vxx + (1-t) cos 51Tx -6cos 1x - 3k + 1 Problem B.C. : Vx (0, t) = 0 Vx (5, 4)=0 I.C. : V (x,0) = 9 cos 21 x - 4cos Flix + 2 V. (x,0) = -3cos 7Tix + 23\ffor n = 1, 2, 3, ... F. = 2 F. (x,4) . X, (x) dx = (1-t) | cos (STx) cos (fux) dx -6cos (21 x ) cos (am x )dx - 3t [ cos* * * ) ax + [ ( ) ax ] = [(1-E) ['cos (5Tx) cos( ATT x ) dx - 6[ cos( 74 x) cos(24 x)dix (1 - E ) if A = 25 if a# 25, 0 # 7 *. = = [ f.(x 4) . X (xlax = [9 / cos (2Tx) cos ( X x) dx - 4 [cos ( x) cos (I x )dx + 2 [ios (eds ) dx ] 0 if a$ 10 , 1# 7 9,3 2 [,3. (x,E) . X.(x)dx = ] [-3/ cos (71x) cos (#x)dx + 23 [cos/tax) dx] = 18 \\ " # 35 if n = 25 : V 25 + 3 (5TT) # V25 = (1-) : V25 (t ) = [(1-t) sin (5TIV3 (t-() d't V25 (0) = 0 V25 (0 ) = 0 = = (1-k) 75 Tri (-1 + cos (5TTV/3 #+))\f\f6. Find the solution of the problem u(x, (). Dare: 11 ( n, r ) = v ( mt) - (x-5 ) " sinnt + 2"t :-1+3+ 142 +23+ +2 - (1 -+2 1-1 + cos (5 013+ ] cossnim + 9 cos ( 2 n13+ ) . cosina + 50 [-1 reos Taft ] . 49 12 Cos In n + 4 cos Tom - 3 gin ( 1053 + ) . Cosinn 5 - ( 2 - 5 ) first 1 2 27 u ( n , + ) = - 1 4 3 + + + 23 + + 2 - ( 1 - 1) [ - 1 + cos ( or 3t ] coston 75 n> + 9 cos ( 29134 ) . cos 201m . 10 5 Cos Inx + 4 cosmo x - 3 sir ( 70 53 + ) . colTom - $ ( m' -10x + 25 ) sin 217. Verify u(x, t) Date: Verify u ( x . " ) WH = 3 Van + ( 1 -+)cosshin - beosina - 3+ +1 U . ( 5, + ) = 101 u ( x, 0 ) = q cos ( 20 m) - 4 cos JA n +2 U . ( 2 0) 2 - 3 cos ( 717m) + 1071 - 2 6. ( : U.(or1) - Valot) - ( m-( ) sinst rant = 01 5 sinat + 0 Un ([, A) = VM ( s, + ) - ( n - 5) sinst rent 20 -0 + 10 + J . ( : u ( m, 0) = 9 cos ( 2 0m ) - 4005 ( 70 n ) 12 U . ( 7 , 0 ) = V . ( n, 0 ) - be-()? cost rot? = 23 - 3 cos ( 7mix ) - ( x-5 )212 . =23 - 3 cos ( 71x ) -2XHUm- 20175 = - 3 cos 70m Flow - 28) Draw the graph u(x, 10) Graph u (x1, 10) U (x, 10) = -(1-10)[-1 + Cos(5#13 (10)/ cos 5x x + 9 cos ( 2#/3 (10)) Cos 2RX 75 x + 50 [ -1 + cos 7 753 1017. Cox 7x x+ 4 cos 78 x - 3 sin (7 XJ3(10.) . cos 72 x - (10)3+1(10)2+23 (10)+2 -I (x 2-10x+25) =in2(D'+ x"(10) 2 u (2, 10) = 0. 0117 cos (5xx3- 2. 905 cos 271 x - 0. 0787 cos Zx x+ 4 095 24 x FOOT -10701 cos 7RX + 9.829 x2 + 1.710x - 222.275 X U(X/10) ULXAD) 0 - 222.275 -215 794 200 2 -189 . 657 - 143 86 4 -72 404 5 6.70s 1 3 -200 - 30019) Draw the graph u(3, (), time interval 0 Displacement of the left hand end of the string is equal 0 and displacement of the right hand end of the string is equal cost. > At initial form of the string is given as 3sin 11nx + 5sin + 8 At initial speed is equal 7sin 8 + 8sing There is a force acting on the string expressed by the function 7nx X 7 sin -cost 8 Your task followings: 1. Specify the problem as mathematical model. Problem for u(x, t). 2. Write appropriate Transformation v(x, t) for the Step 1. 3. Finalize Step 1 and specify the problem for v(x, t). 4. Find v(x, t). 5. Find the solution of the problem u(x, t). 6. Draw the graph (x, 10) . 7. Draw the graph u(1, t) , 0