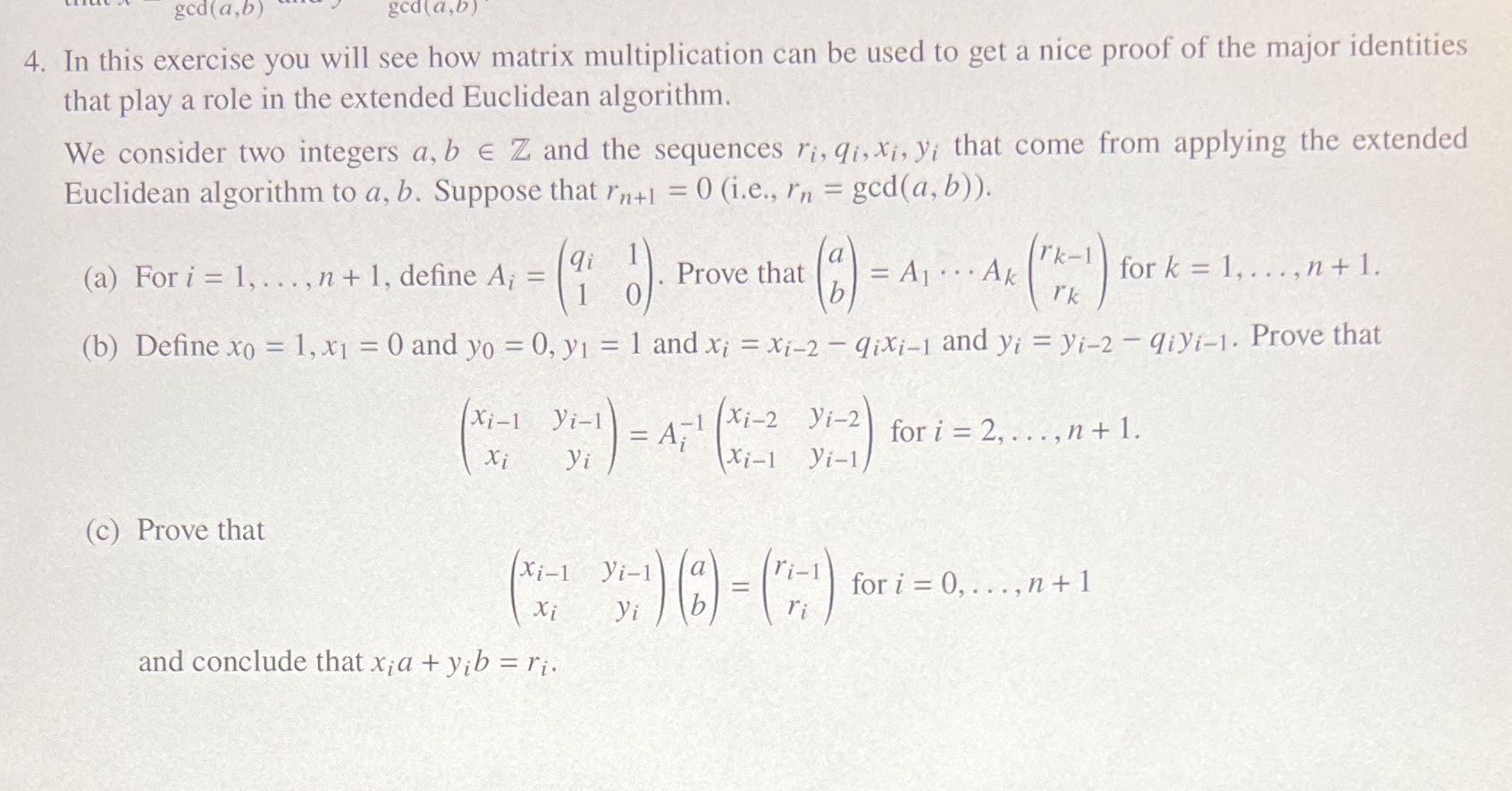
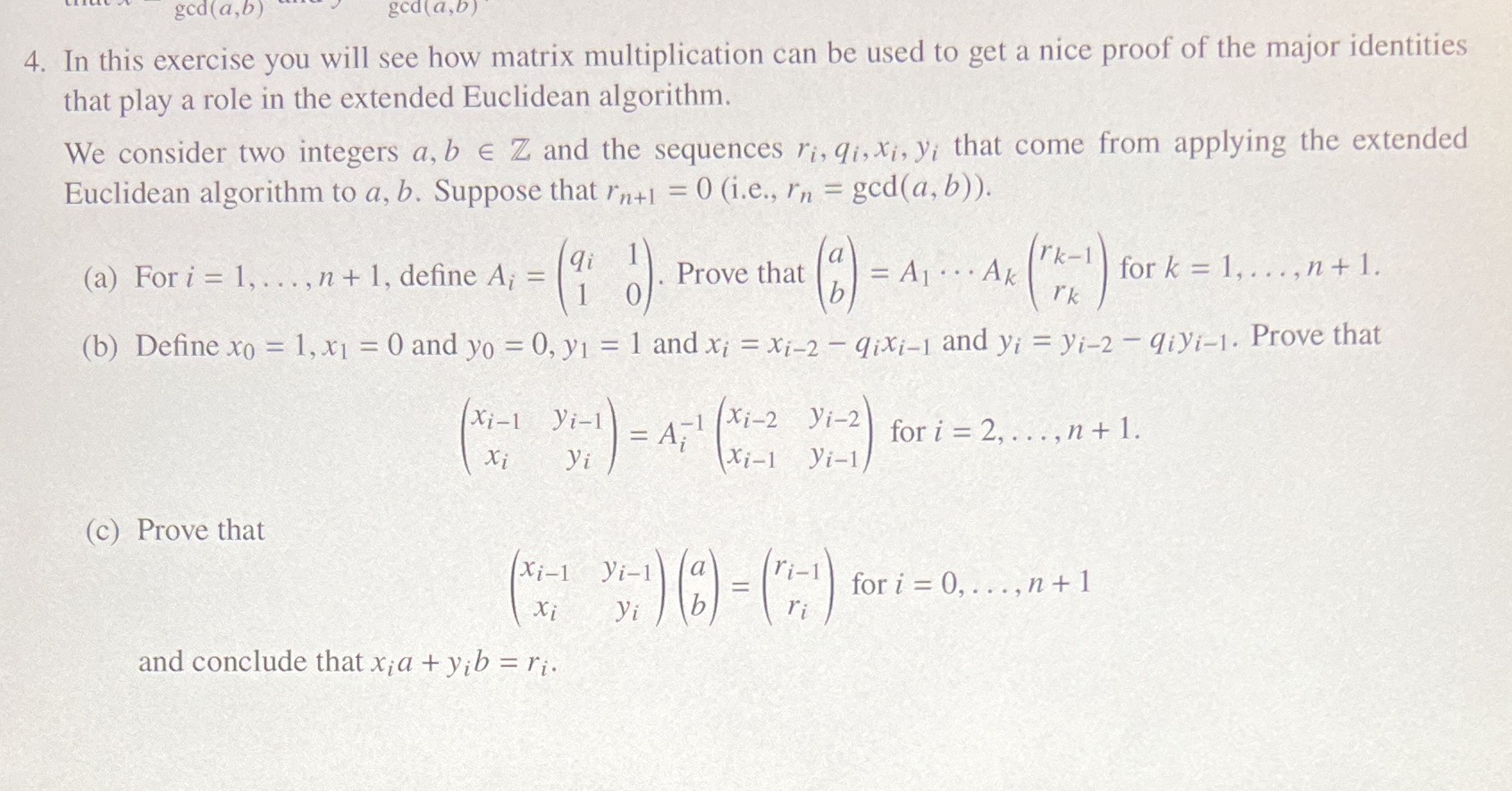
god (a,b) gca ( a,b) 4. In this exercise you will see how matrix multiplication can be used to get a nice proof of the major identities that play a role in the extended Euclidean algorithm. We consider two integers a, b E Z and the sequences ri, qi, xi, yi that come from applying the extended Euclidean algorithm to a, b. Suppose that In+1 = 0 (i.e., In = god(a, b)). (a) For i = 1, . .., n + 1, define A; = qi Prove that = A1 . . . Ak rk-1 for k = 1, ..., n + 1. rk (b) Define xo = 1, x1 = 0 and yo = 0, y1 = 1 and xi = Xi-2 - qixi-1 and yi = yi-2 - qiyi-1. Prove that Xi-1 yi-1 = A; Xi-2 yi-2 for i = 2, . .., n + 1. xi yi Xi=1 yi-1/ (c) Prove that Xi-1 yi-1 Xi yi (6) ="for i = 0,..,n + 1 and conclude that xia + yib = ri