GRADE 9---

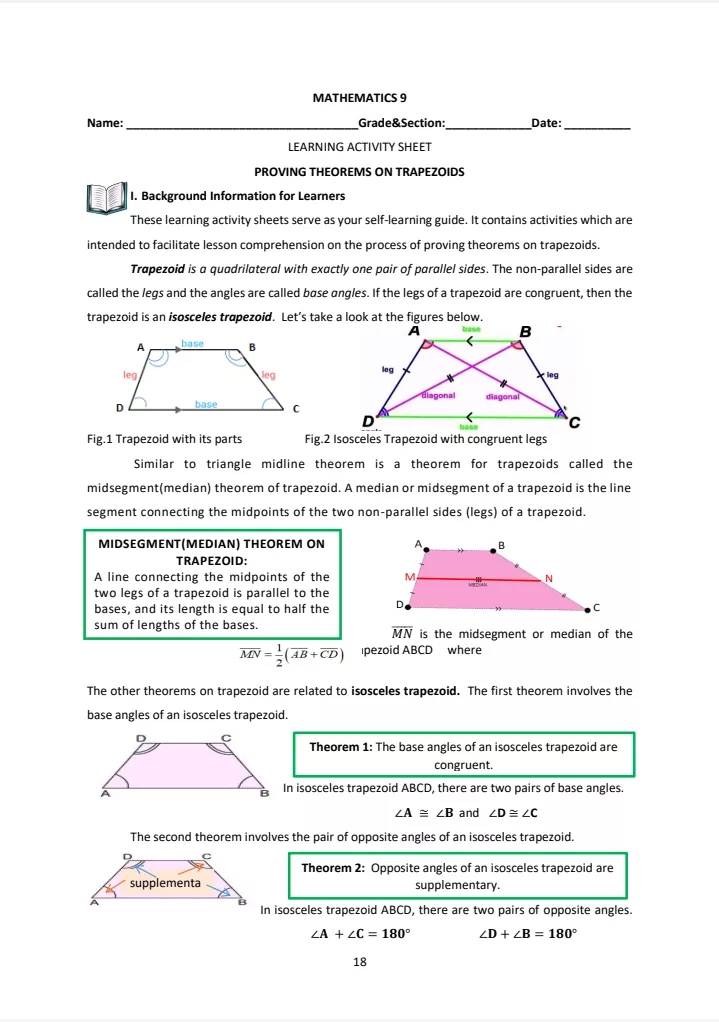
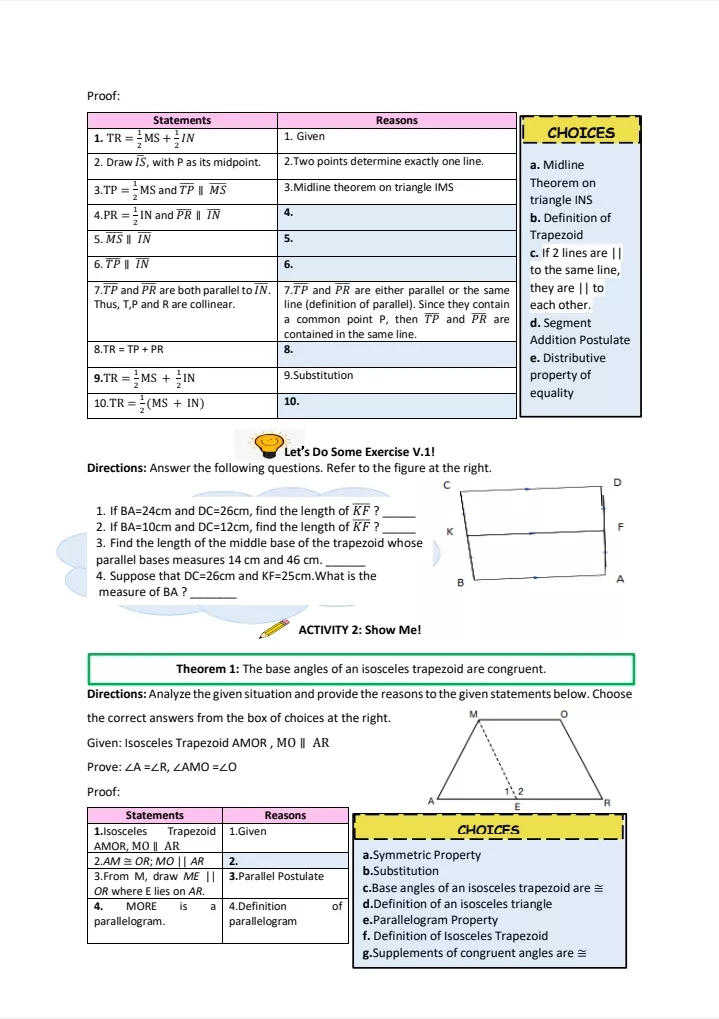
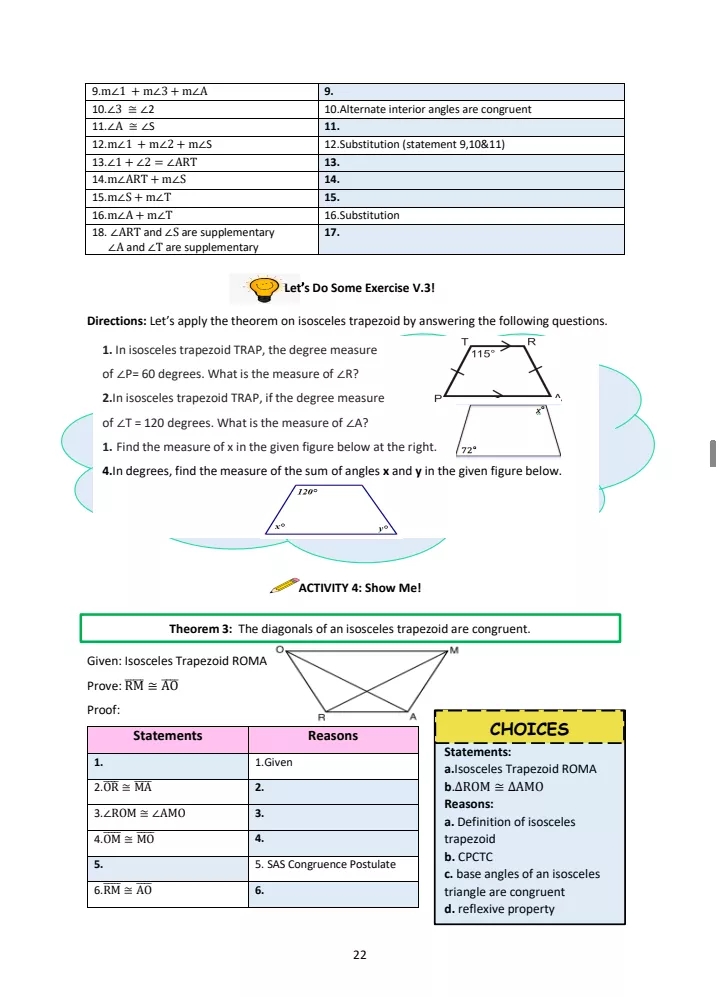
MATHEMATICS 9 Name: Grade&Section: Date: LEARNING ACTIVITY SHEET PROVING THE MIDLINE THEOREM I. Background Information for Learners These activity sheets serve as your self-learning guide and will facilitate the lesson on proving the midline theorem. Proving the midline theorem is very useful in helping us understand some of the concepts in geometry especially in connection with trapezoid and similarity. For us to prove the midline theorem, let's first know what the midline theorem is. MIDLINE THEOREM: In AABC, D and E The segment that joins are midpoints of AB and AC E the midpoints of two sides of a respectively. These midpoints triangle is parallel to the third side when joined makes segment and half as long. DE C The following definitions of some important terms may be of help to you: Definition of Midpoint - A point on a line Definition of Midpoint |AM = segment that divides it into two equal parts. M E The halfway point of a line segment. SAS (Side-Angle-Side) Congruence Postulate - states that if the two sides and an included Side-Angle-Side Postulate angle of one triangle are congruent to the If: 2 sides and an included angle corresponding two sides and the included are congruent angle of another triangle, then the triangles are congruent The AIP Theorem - If two lines form congruent alternate interior angles with a transversal, then the lines are AIP parallel. CPCTC - Corresponding Parts of Congruent Triangles are Congruent Vertical Angles - two nonadjacent angles CPCTC formed by two intersecting lines. Transitive property of congruence - AB = CD and CD = EF, then AB R ~ EF AXYZ . ATRS Segment addition postulate - states that if we are given two points on a line segment, A and C, a third point B lies on the line segment AC if and only if the distances between the points meet the requirements Vertical Angles or of the equation AB + BC = AC. (You may also review definition of other terms, AB + BC = AC algebraic properties, postulates, and theorems that may help you accomplish the given activities.) 14Il. Learning Competency: Proves the midline theorem (for triangles). (M9GE-Illd-1) ACTIVITY 1: It's Paperellelogram! Let three family members or friends join when you do the activity. Prepare the materials needed. Follow the procedure and answer the questions given. Materials: 4 pieces of short bond paper, pencil, ruler, adhesive tape, protractor, and scissors. Procedure: 1. Each member shall draw and cut a different kind of triangle out of a bond paper. (equilateral triangle, right triangle, obtuse triangle, and acute triangle that is not equiangular.) 2. Choose a third side of a triangle. Mark each midpoint of the other two sides then connect the midpoints to form a segment. 3. Measure the segment drawn and the third side you chose. Q:Compare the lenghts of the segments drawn and the third side you chose. What did you observe? 4. Cut the triangle along the segment drawn. Q:What two figures are formed after cutting the triangle along the segment drawn? 5. Use an adhesive tape to reconnect the triangle with the other figure in such a way that their common vertex was a midpoint and that congruent segments formed by a midpoint coincide. Q:After reconnecting the cutouts, what figure new figure is formed? Why? Q:What can you say about your findings in relation to those of your family members/friends? Q:Do you think that the findings apply to all kinds of triangles? Why? ACTIVITY 2: Show Me! Directions: To prove the midline theorem, analyze the given situation below and provide the reasons to the given statements that follow. You can choose the correct answers from the box of choices at the right. MIDLINE THEOREM: The segment that joins the midpoints of two sides of a triangle is parallel to the third side and half as long. Given: AHNS, O is the midpoint of HN, E is the midpoint of NS Prove: OE | HS, OE = = HS 15 HProof: Statements Reasons CHOICES 1. AHNS, O is the midpoint of HN, 1.Given E is the midpoint of NS a. Definition of 2. When Of is extended. There is a 2.In a line there is a exactly one point between parallelogram. point T such that OE = ET two other points that is considered as the midpoint of the line. And these two points are b. SAS equidistant to the midpoint Congruence 3. EN = ES 3. Postulate 4. 42 = 23 4. Vertical Angles are Congruent 5. AONE = ATSE 5. c. Parallelogra 6. 21 = 24 6.CPCTC m Property. 7. HN II ST 7. d. Definition 8. OH = ON 8. Definition of Midpoint of Midpoint 9. ON = TS 9. CPCTC(Statement 5) 10. OH = ST 10. e. Substitution 11. Quadrilateral HOTS is a 11. [statement parallelogram. (SN) 2] 12. DE II HS 12.0E is on the side of OT of HOTS 13. OE + ET = OT 13.Segment Addition Postulate (SAP) F. Addition 14. OE + OE = OT 14. 15. 20E = OT 15. g. By AIP Theorem 16. HS II OT 16. 17. 20E = HS 17. By Substitution h. Substitution 18. OF = =HS(The segment joining 18. (SN 14 and 15) the midpoints of two sides of a triangle is half as long as the third i. Transitive side. Property Congratulations! You've just completed the proof of the midline theorem. This theorem can be applied to solve problems. Try the activity that follows. ACTIVITY 3: Go for It! Directions: In AMCG, A and I are the midpoints of MG and CG, respectively. Consider each given information and answer the questions that follow. 1. Given: Al=5.5 Question: What is the measure of MC? 2.Given GC= 8 Question: What is the measure of CI ? 3. Given GI= 4 and MA = 5 Question: What is the measure of MG? GC? MG + GC? 4.Given Al= 17 Question: What is the measure of Al + MC? 16RUBRIC FOR ACTIVITY 1: It's Paperellelogram! 4 points 3 point 2 points 1 point A complete response to |Good solid response Explanation is Misses key Understanding questions with detailed with clear unclear. points. explanation. explanation. Shows complete Response shows Response shows Shows substantial Demonstrated understanding of the understanding of the some complete lack questions of knowledge understanding of mathematical ideas and problem, ideas and understanding processes. the task. processes of the task Does not meet Goes beyond the Meets the Hardly meets the the Requirements requirements of the requirements of the requirements of requirements of task. task the task. the task REFERENCES REFLECTION Bryant, M.L., Bulalayao, L. E., Callanta, M.M., Cruz, J.D., De Vera, R.F., Garcia, G.T., Javier, S.E.,Lazaro, R.A., What is your "hugot line" to Mesterio, B.J. & Saladino, R.H.A,(2014), Mathematics Learner's Material 9, FEF Printing Corp. express your feelings while https:/calculators.com/geometry/mid-points- answering the activities. calculator.htm https://virtualnerd.com/geometry/congruent- triangles/proof-sss-sas/definition-sas-triangle- congruence-postulate https://slideplayer.com/slide/14709210/ https://www.learner.org/series/learning-math- geometry/dissections-and-proof/part-c-the-midline- theorem-55-minutes/ 15.f D'9T 11.2 14.6 2.4 18.1 !'OT 1.11 vary) Activity 3: Activity 2: 1. MG=10 Activity 1: Answer Key 8:09 (Answers may Prepared by: CRISTINE R. OPIANA Writer 17MATHEMATICS 9 Name: Grade&Section: Date: LEARNING ACTIVITY SHEET PROVING THEOREMS ON TRAPEZOIDS I. Background Information for Learners These learning activity sheets serve as your self-learning guide. It contains activities which are intended to facilitate lesson comprehension on the process of proving theorems on trapezoids. Trapezoid is a quadrilateral with exactly one pair of parallel sides. The non-parallel sides are called the legs and the angles are called base angles. If the legs of a trapezoid are congruent, then the trapezoid is an isosceles trapezoid. Let's take a look at the figures below. A base leg leg diagonal diagonal base D' Fig.1 Trapezoid with its parts Fig.2 Isosceles Trapezoid with congruent legs Similar to triangle midline theorem is a theorem for trapezoids called the midsegment(median) theorem of trapezoid. A median or midsegment of a trapezoid is the line segment connecting the midpoints of the two non-parallel sides (legs) of a trapezoid. MIDSEGMENT (MEDIAN) THEOREM ON TRAPEZOID: A line connecting the midpoints of the M two legs of a trapezoid is parallel to the bases, and its length is equal to half the D sum of lengths of the bases. MN is the midsegment or median of the MN = (4B +CD) ipezoid ABCD where The other theorems on trapezoid are related to isosceles trapezoid. The first theorem involves the base angles of an isosceles trapezoid. Theorem 1: The base angles of an isosceles trapezoid are congruent. In isosceles trapezoid ABCD, there are two pairs of base angles. ZA = 2B and ZD = ZC The second theorem involves the pair of opposite angles of an isosceles trapezoid. Theorem 2: Opposite angles of an isosceles trapezoid are supplementa supplementary. In isosceles trapezoid ABCD, there are two pairs of opposite angles. ZA + 2C = 180