Graph:

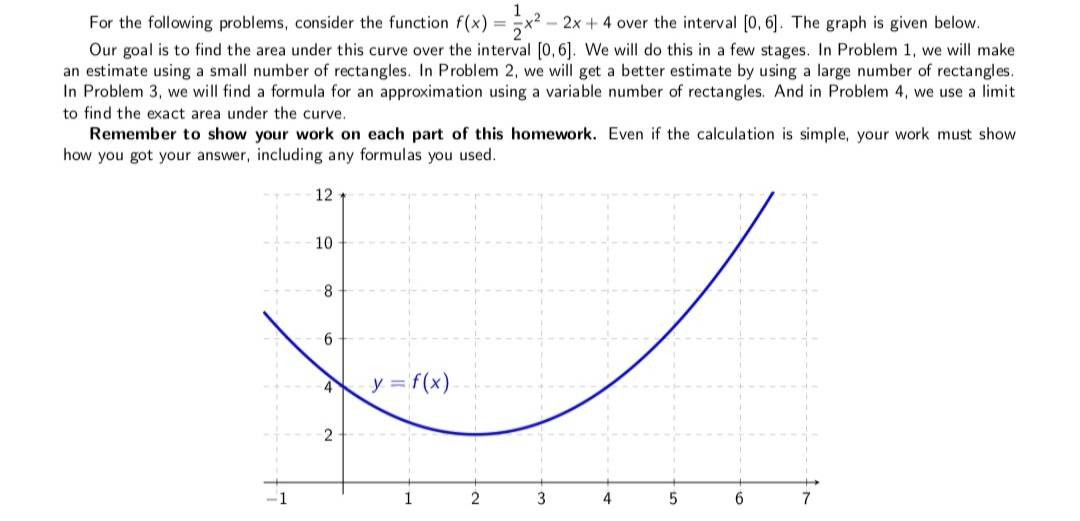
Problem 3: Finding a Formula for an Approximation with a Variable Number of Rectangles {13 points) If you want to evaluate many different approximations of the same function. you can leave the number of rectangles as a variable n. The process of finding the approximation is the same as abOve. but the final answer will have the n variable left. This problem will walk you through this process. a} (2 points} Find a formula for the width. Ax. of each rectangle used in this approximation. x: b) (3 points} Find a formula for the grid point xk. (The only variables appearing in your expression should be k and n.) X 2- | c} (2 points} Find a formula for the sample point Kg. (The only variables appearing in your expression should be it and n. Remember that we are using right endpoints.) r> Dc: of the Riemann sum found in Problem 3(f} above. (Your final answer should have no variables left in it. Don't forget to check the form and show your work. You may use I'Hopital's Rule.) Limit Value: c} (2 points} Explain what the value of this limit from part (b) represents in the context of this problem. Be as specific as you can (i.e. do not say "the function". instead give the name of the function.)