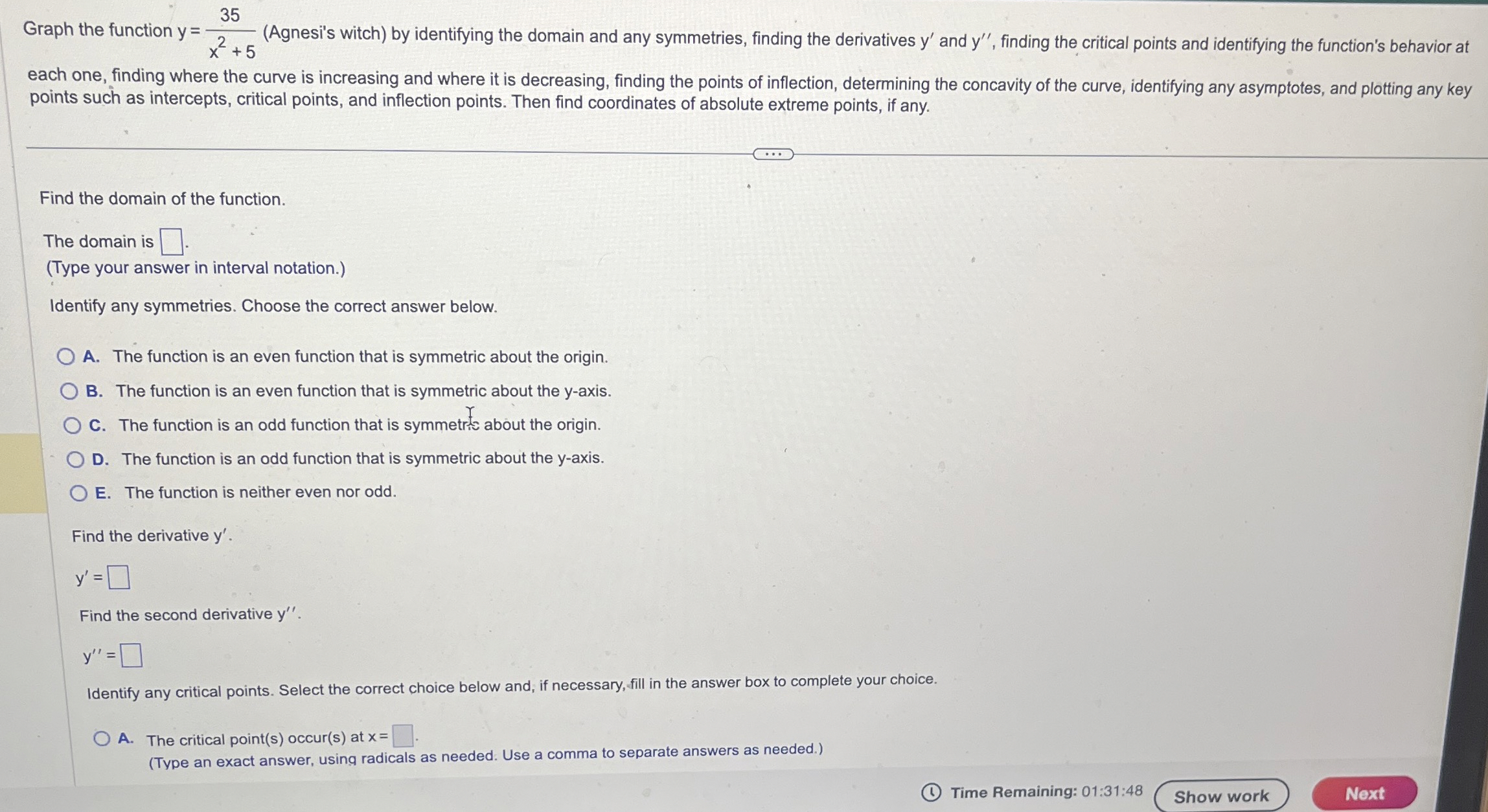
Question: Graph the function y = 3 5 x 2 + 5 ( Agnesi ' s witch ) by identifying the domain and any symmetries, finding
Graph the function Agnesis witch by identifying the domain and any symmetries, finding the derivatives and finding the critical points and identifying the function's behavior at each one, finding where the curve is increasing and where it is decreasing, finding the points of inflection, determining the concavity of the curve, identifying any asymptotes, and plotting any key points such as intercepts, critical points, and inflection points. Then find coordinates of absolute extreme points, if any.
Find the domain of the function.
The domain is
Type your answer in interval notation.
Identify any symmetries. Choose the correct answer below.
A The function is an even function that is symmetric about the origin.
B The function is an even function that is symmetric about the axis.
C The function is an odd function that is symmetr about the origin.
D The function is an odd function that is symmetric about the axis.
E The function is neither even nor odd.
Find the derivative
Find the second derivative
Identify any critical points. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A The critical points occurs at
Type an exact answer, using radicals as needed. Use a comma to separate answers as needed.
Time Remaining: ::
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


