Graphs & greedy algorithms

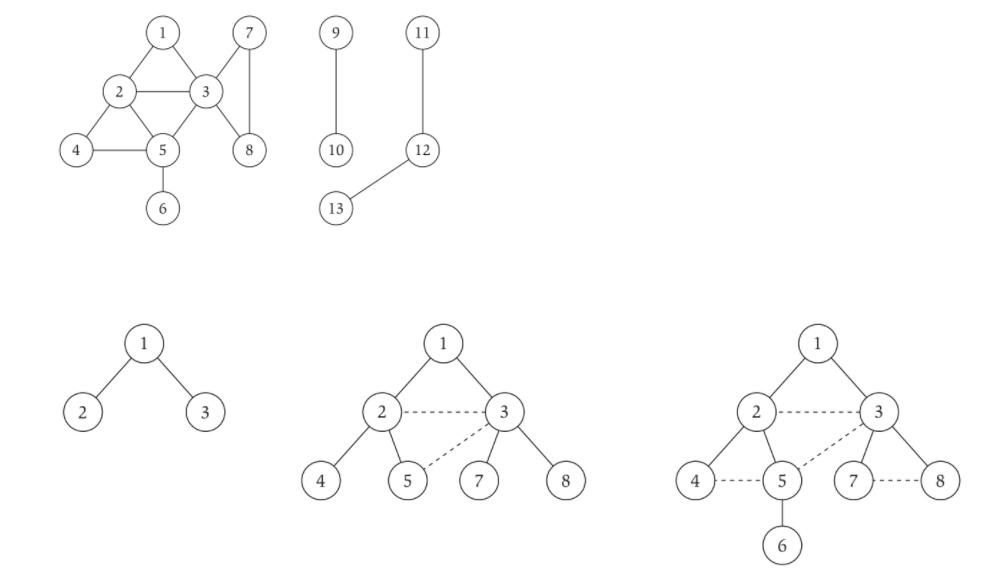
Use one tree to show the tracing of the breadth first algorithm given in L4 for solv- ing the LAX - LGA connectivity problem (recall s-t connectivity problem defined in class) in the graph given in Question 1. For an example, see the rightmost tree above section 4.1 in L4. You only need to draw the final tree, and no need to draw the dotted lines. Note any node will occur in your tree at most once. 4. S-t connectivity problem Suppose we are given a graph G = (V, E) and two particular nodes s and t. We'd like to find an efficient algorithm that answers the question: Is there a path from s tot in G? We will call this the problem of determining s-t connectivity. 11 4 8 10 12 13 2 3 2 4 5 8 4 5 7 8 6 4.1 Breadth first search algorithm Example: 1-6 connectivity problem 1 2, 3 Algorithm (Function) Name: breadth Search Input G=(V, E) a graph S, starting node t, terminating node Output hasPath = true: there is a path from s tot = false otherwise Side effects N.A. Auxiliary data Q: a queue II a node in the queue means its neighbors need to be inspected // visited[i]: 0 means i is not visited, 1 otherwise Plan 1. put s into Q, and hasPath := false 2. while Q is not empty 3. take/remove the first element u from Q 4. if u ist 5. hasPath := true 6. break 7. else 8. mark u as visited 9. for each {u, v} \in E Il put the un-visited neighbors of u into Q 10. if v is not visited 11. put v into Q End of algorithm === 03/04/21 discussion about complexity of the algorithm === Observation: every node can but put into Q at most once Steps of for loop in line 9 is # of neighbors of node u (total steps: sum of the degree of every node) Step: 2*e (e is the number of edges of the graph) bigO(e) ===