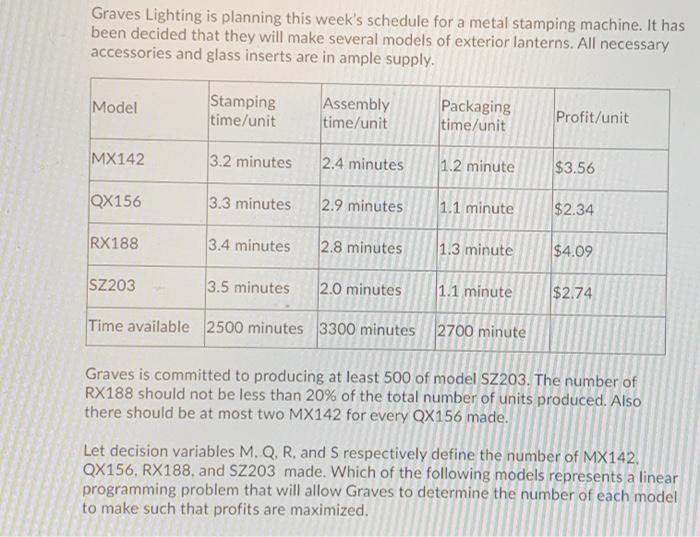
Graves Lighting is planning this week's schedule for a metal stamping machine. It has been decided that they will make several models of exterior lanterns. All necessary accessories and glass inserts are in ample supply. Model Stamping time/unit Assembly time/unit Packaging time/unit Profit/unit MX142 3.2 minutes 2.4 minutes 1.2 minute $3.56 QX156 3.3 minutes 2.9 minutes 1.1 minute $2.34 RX188 3.4 minutes 2.8 minutes 1.3 minute $4.09 SZ203 3.5 minutes 2.0 minutes 1.1 minute $2.74 Time available 2500 minutes 3300 minutes 2700 minute Graves is committed to producing at least 500 of model SZ203. The number of RX188 should not be less than 20% of the total number of units produced. Also there should be at most two MX142 for every QX156 made. Let decision variables M. Q, R, and respectively define the number of MX142. QX156, RX188, and SZ203 made. Which of the following models represents a linear programming problem that will allow Graves to determine the number of each model to make such that profits are maximized