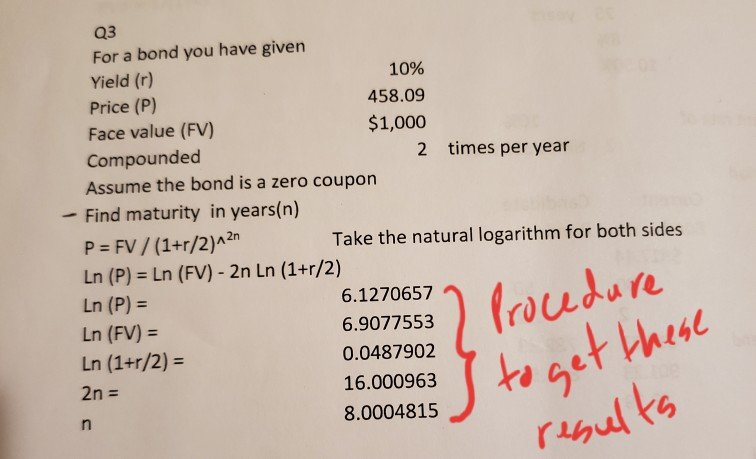
Greetings, I recently received your help for this exercise, but you only told me how to get one of the results. Could you help me by explaining how to get each of the results given? thank you very much for your attention.

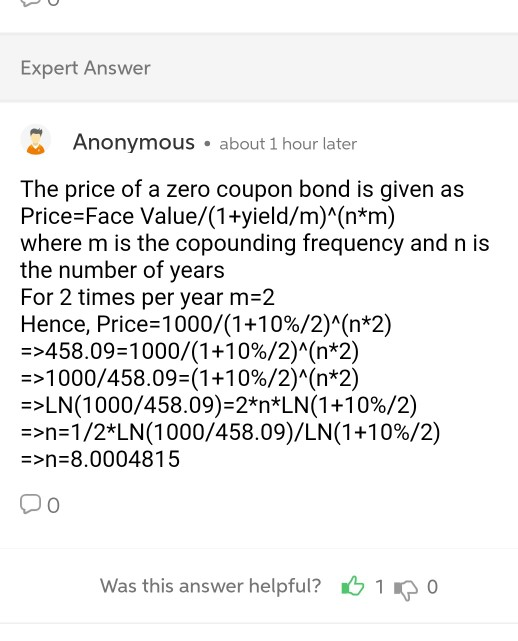
Q3 For a bond you have given Yield (r) 10% Price (P) 458.09 Face value (FV) $1,000 Compounded 2 times per year Assume the bond is a zero coupon - Find maturity in years(n) P = FV / (1+r/2)^21 Take the natural logarithm for both sides Ln (P) = Ln (FV) - 2n Ln (1+r/2) In (P) = 6.1270657 Ln (FV) = 6.9077553 Ln (1+r/2) = 0.0487902 2n = 16.000963 8.0004815 6.9077553) Procedure to get these results Expert Answer Anonymous about 1 hour later The price of a zero coupon bond is given as Price=Face Value/(1+yield/m)^(n*m) where m is the copounding frequency and n is the number of years For 2 times per year m=2 Hence, Price=1000/(1+10%/2)^(n+2) =>458.09=1000/(1+10%/2)^(n*2) =>1000/458.09=(1+10%/2)^(n*2) =>LN(1000/458.09)=2*n*LN(1+10%/2) =>n=1/2*LN(1000/458.09)/LN(1+10%/2) =>n=8.0004815 DO Was this answer helpful? B1100