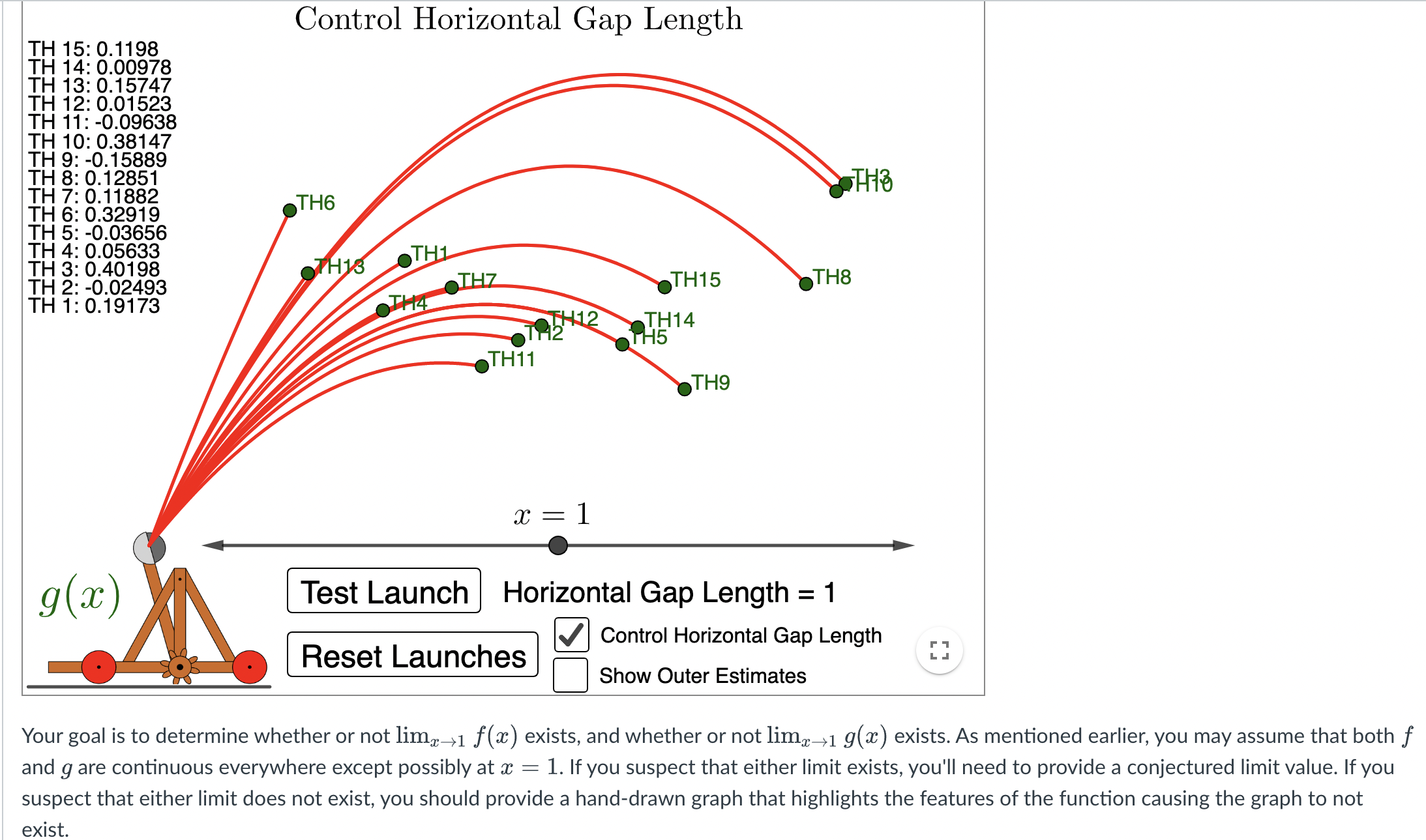
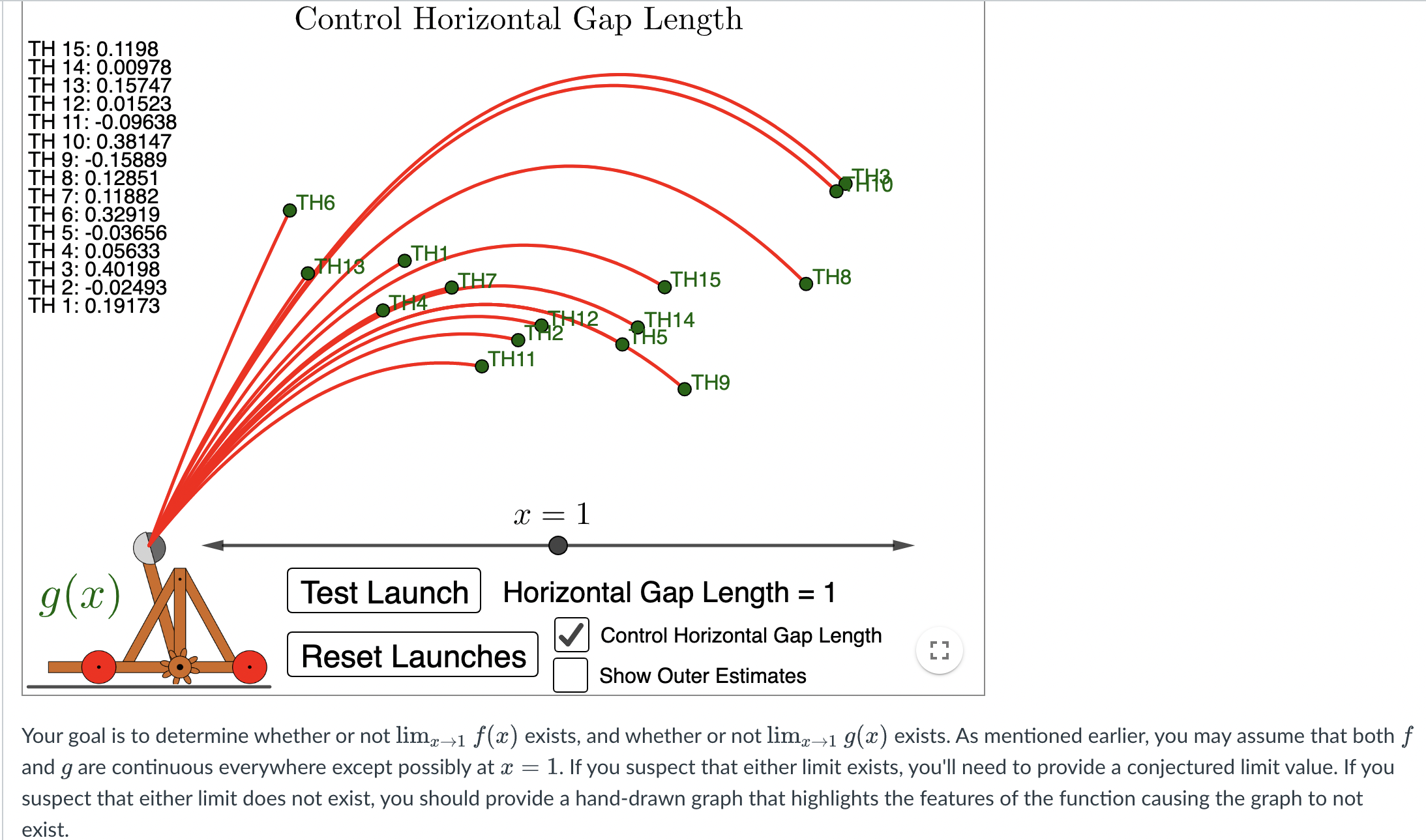
Guiding Question 1: What is the smallest possible max error (i.e., the distance between the highest overestimate and the lowest underestimate from the function data) over the gap of size 1? Guiding Question 2: What is the smallest possible max error (i.e., the distance between the highest overestimate and the lowest underestimate from the function data) over the gaps of size .5 and .1? Guiding Question 3: Is there a gap size that lets all of the function's values can t within a max error of .5? Guiding Question 4: Is there a gap size that lets all of the function's values can t within max errors of .1 and .01? Guiding Question 5: If the function's values continue to behave as modeled in the applet (i.e., beyond the computational capacity of the applet), will we be able to nd a small enough gap size to satisfy any small error bound? Control Horizontal Gap Length TH 15: 0.1198 TH 14: 0.00978 TH 13: 0.15747 TH 12: 0.01523 TH 11: -0.09638 TH 10: 0.38147 TH 9: -0. 15889 TH 8: 0. 12851 TH 7: 0.11882 THO TH 6: 0.32919 TH6 TH 5: -0.03656 TH 4: 0.05633 TH 3: 0.40198 THIS OTH1 TH 2: -0.02493 OTHZ TH15 TH8 TH 1: 0.19173 TH12 TH14 12 TH5 TH11 TH9 x = 1 g (x ) Test Launch Horizontal Gap Length = 1 Control Horizontal Gap Length Reset Launches V Show Outer Estimates Your goal is to determine whether or not limx->1 f(a) exists, and whether or not limx->1 9(x ) exists. As mentioned earlier, you may assume that both f and g are continuous everywhere except possibly at * = 1. If you suspect that either limit exists, you'll need to provide a conjectured limit value. If you suspect that either limit does not exist, you should provide a hand-drawn graph that highlights the features of the function causing the graph to not exist