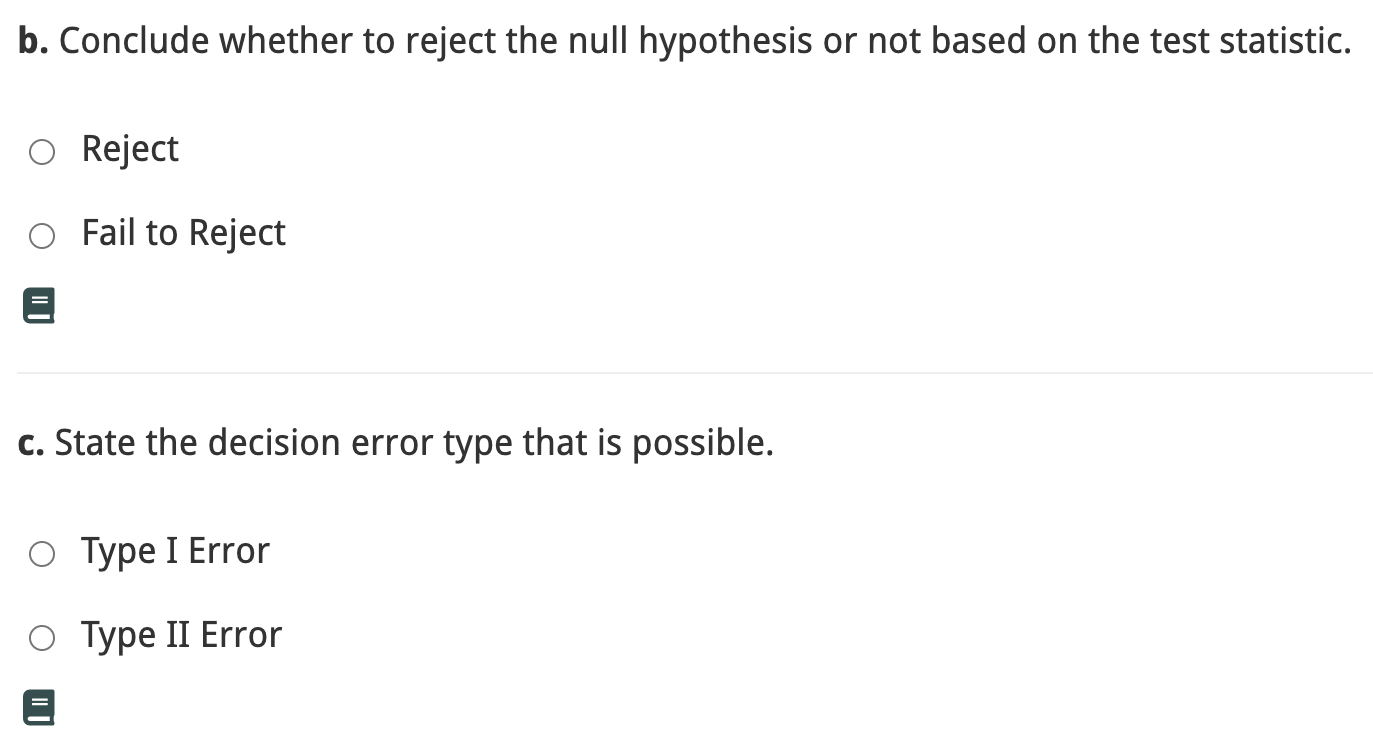
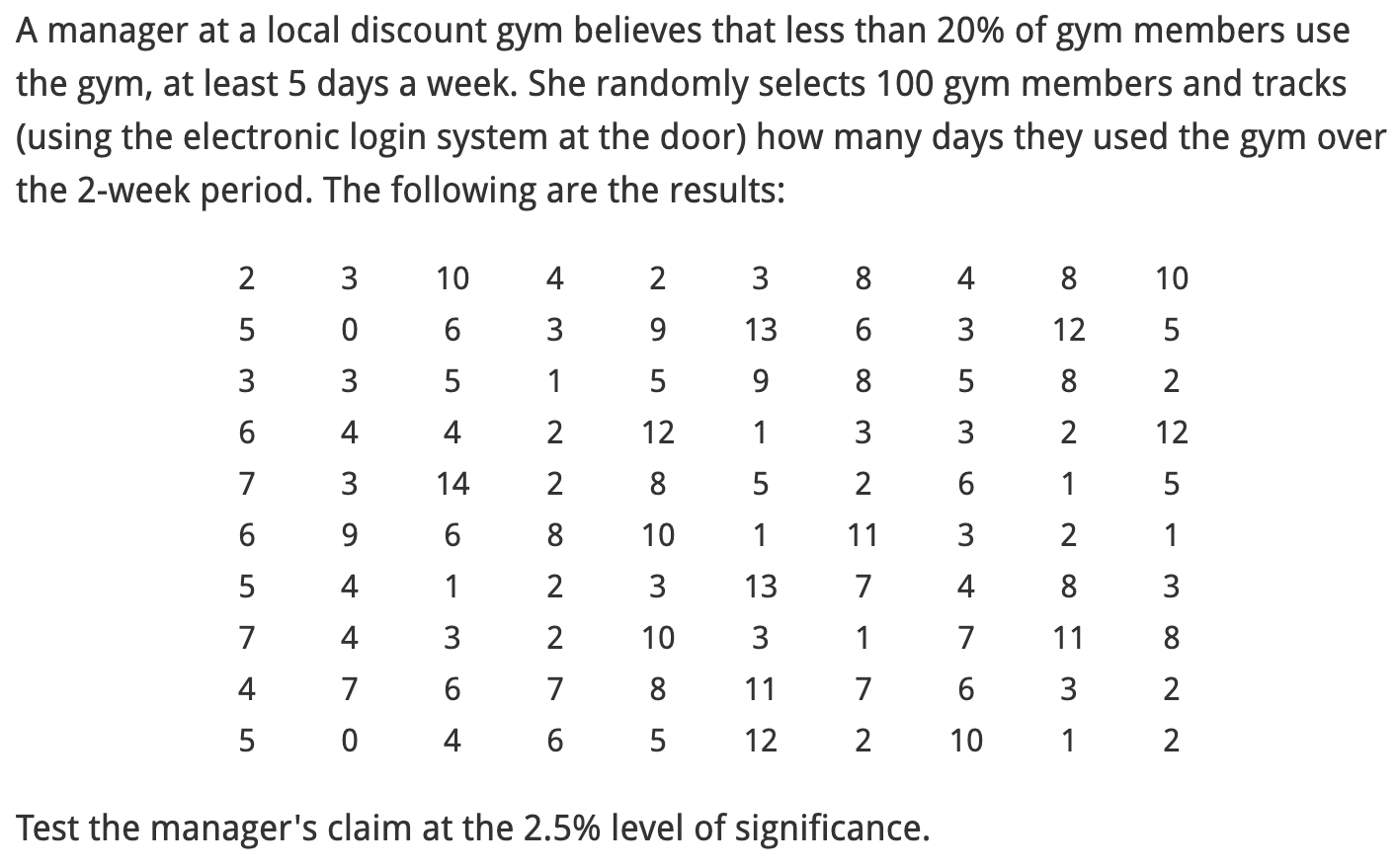
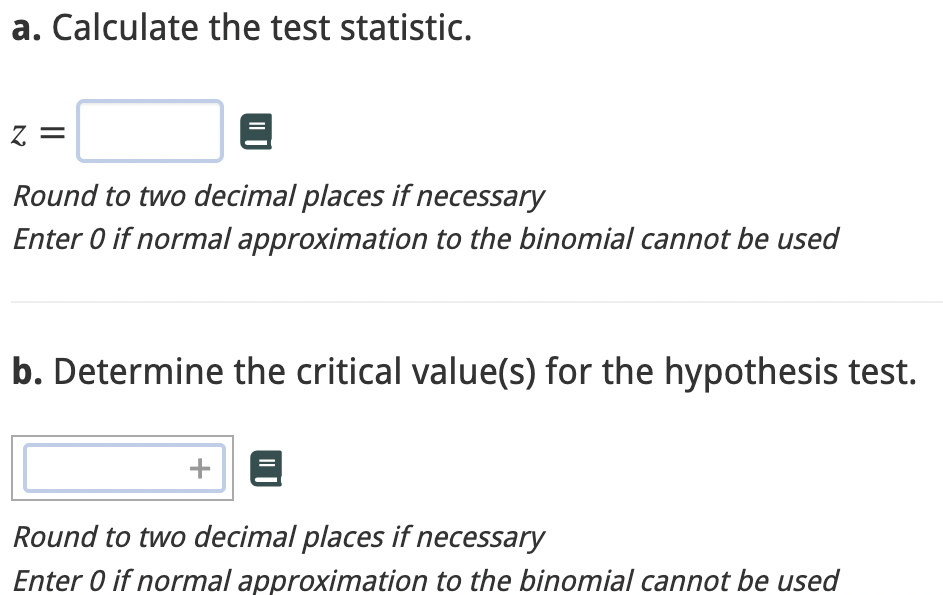
H0 : p = 14 kg H1 : p > 14 kg Level of significance: 0: = 0.05 Sample size: n = 36 Test statistic: t = 1.031 Unknown population standard deviation ' T-Distribution Table a. Determine the critical value(s) for the proposed hypothesis test. _5 Round to three decimal places if necessary b. Conclude whether to reject the null hypothesis or not based on the test statistic. O Reject O Fail to Reject E c. State the decision error type that is possible. 0 Type I Error 0 Type 11 Error E Test the claim that the average weight of a new SUV is 1,940 kg, if a sample of 290 vehicle weights results in a sample mean of 1,931 kg, with a standard deviation of 61 .7 kg. Use a 20% level of significance. I Standard Normal Distribution Table I a. Calculate the test statistic. z= 5 Round to two decimal places if necessary b. Determine the critical value(s) for the hypothesis test. -5 c. Conclude whether to reject the null hypothesis or not based on the test statistic. O Reject O Fail to Reject E Determine if the conditions required for the normal approximation to the binomial are met. If so, calculate the test statistic, determine the critical value(s), and use that to decide whether there is sufficient evidence to reject the null hypothesis or not at the given level of significance. Ho : p = 0.139 H1 : p