Haskell coding question

Please answer the following questions

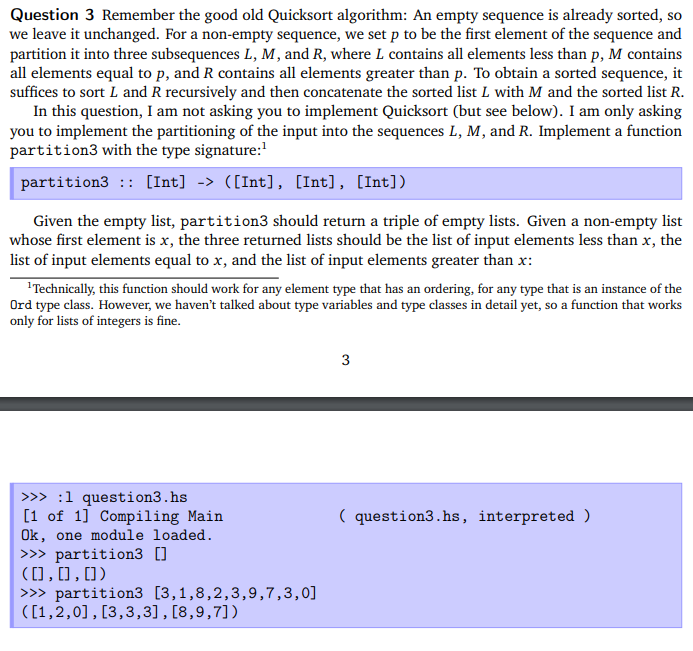
Question 3 Remember the good old Quicksort algorithm: An empty sequence is already sorted, so we leave it unchanged. For a non-empty sequence, we set p to be the first element of the sequence and partition it into three subsequences L, M, and R, where I contains all elements less than p, M contains all elements equal to p, and R contains all elements greater than p. To obtain a sorted sequence, it suffices to sort L and R recursively and then concatenate the sorted list L with M and the sorted list R. In this question, I am not asking you to implement Quicksort (but see below). I am only asking you to implement the partitioning of the input into the sequences L, M, and R. Implement a function partition3 with the type signature: partition3 :: [Int] -> ([Int], [Int], [Int]) 1 Given the empty list, partition3 should return a triple of empty lists. Given a non-empty list whose first element is x, the three returned lists should be the list of input elements less than x, the list of input elements equal to x, and the list of input elements greater than x: Technically, this function should work for any element type that has an ordering, for any type that is an instance of the Ord type class. However, we haven't talked about type variables and type classes in detail yet, so a function that works only for lists of integers is fine. 3 3 ( question3.hs, interpreted ) >>> :1 question3.hs [1 of 1] Compiling Main Ok, one module loaded. >>> partition3 [] ([] , [] , []) >>> partition3 [3, 1,8,2,3,9,7,3,0] ([1,2,0],[3,3,3],[8,9,7]) Question 3 Remember the good old Quicksort algorithm: An empty sequence is already sorted, so we leave it unchanged. For a non-empty sequence, we set p to be the first element of the sequence and partition it into three subsequences L, M, and R, where I contains all elements less than p, M contains all elements equal to p, and R contains all elements greater than p. To obtain a sorted sequence, it suffices to sort L and R recursively and then concatenate the sorted list L with M and the sorted list R. In this question, I am not asking you to implement Quicksort (but see below). I am only asking you to implement the partitioning of the input into the sequences L, M, and R. Implement a function partition3 with the type signature: partition3 :: [Int] -> ([Int], [Int], [Int]) 1 Given the empty list, partition3 should return a triple of empty lists. Given a non-empty list whose first element is x, the three returned lists should be the list of input elements less than x, the list of input elements equal to x, and the list of input elements greater than x: Technically, this function should work for any element type that has an ordering, for any type that is an instance of the Ord type class. However, we haven't talked about type variables and type classes in detail yet, so a function that works only for lists of integers is fine. 3 3 ( question3.hs, interpreted ) >>> :1 question3.hs [1 of 1] Compiling Main Ok, one module loaded. >>> partition3 [] ([] , [] , []) >>> partition3 [3, 1,8,2,3,9,7,3,0] ([1,2,0],[3,3,3],[8,9,7])