Hello all. I really need some help with this physics lab. Thank you

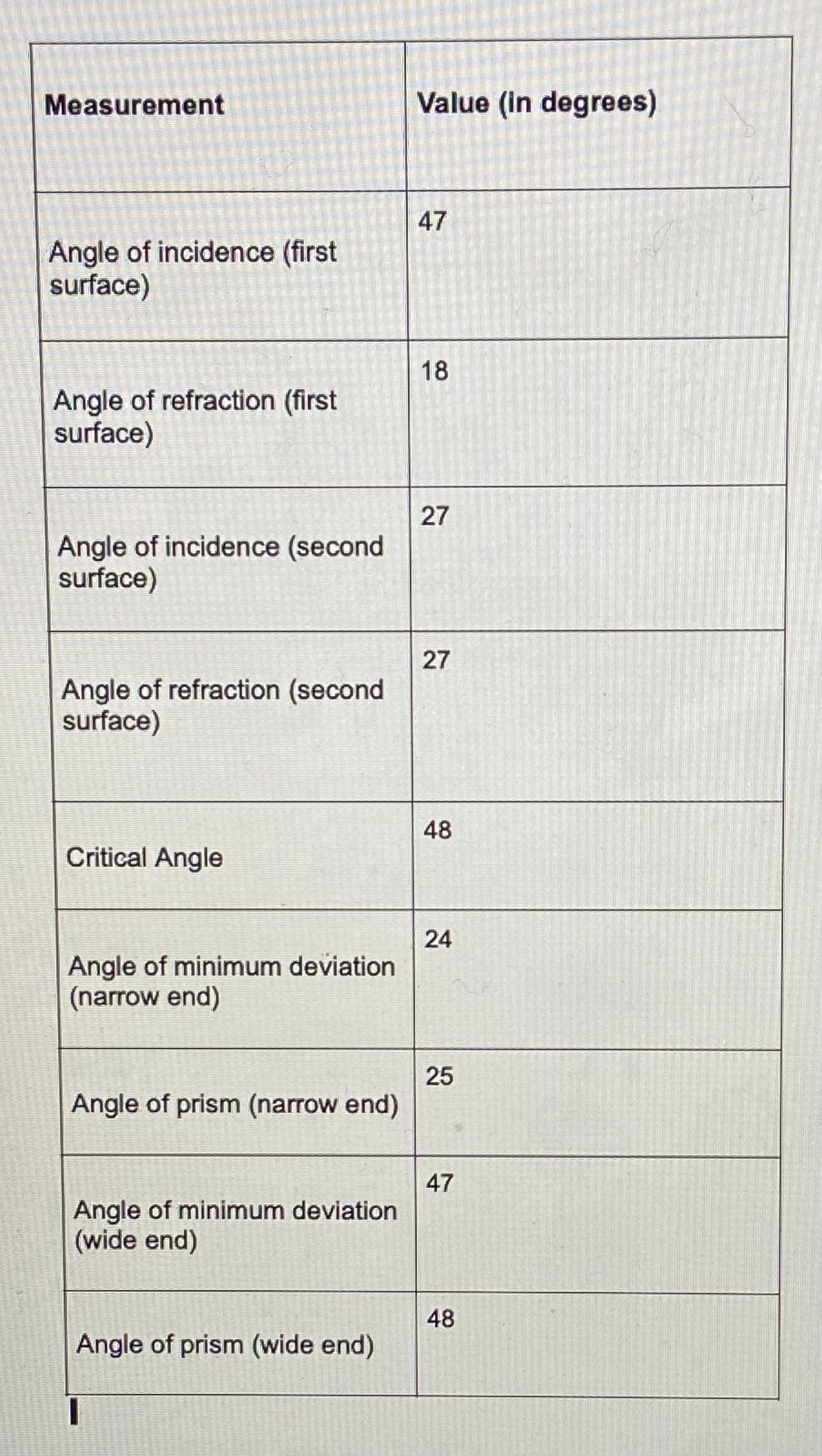
Figure 6.5 Trace of a light ray through the angle of minimum deviationThe transmission of light across a boundary between two media is accompanied by a change in both the speed and wavelength of the wave. This can result in a change of direction at the boundary, a phenomenon known as refraction. In this experiment you measure the change in direction of light beams as they refract or reflect at a boundary to determine the index of refraction of a transparent object. The objectives of this experiment are as follows: 1. To measure the angles of incidence and refraction at a boundary between media 2. To observe total internal reflection at a boundary between media 3. To calculate the critical angle of a boundary between media THEORY Snell's law describes the relationship between the angle of incidence of a beam of light as it intersects a new transparent medium and the angle of refraction as enters that transparent medium. medium 2 medium 1 Figure 6.1 angles of incidence for a light as it intersects a new medium Snell's law quantifies the relationship as shown in equation 6.1. Snell's Law n, sin 8, = n, sin 02 (6.1) Here, 1, is the index of refraction of the initial medium n, is the index of refraction of the new medium 0, is the angle of incidence 0, is the angle of refraction The index of refraction of a medium is the ratio of the speed of light in a vacuum to the speed of light in the medium, as shown in equation 6.2.Measurement Value (In degrees) 47 Angle of incidence (first surface) 18 Angle of refraction (first surface) 27 Angle of incidence (second surface) 27 Angle of refraction (second surface) 48 Critical Angle 24 Angle of minimum deviation (narrow end) 25 Angle of prism (narrow end) 47 Angle of minimum deviation (wide end) 48 Angle of prism (wide end)1. Measure the angles of incidence and refraction at both surfaces of the prism in the tracings of procedures step 2 and 3. Calculate the index of refraction for the Lucite prism from these measurements. 2. Measure the critical angle from the tracing of procedure step 4. Calculate the index of refraction for the Lucite prism from the critical angle. 3. Measure the angle of minimum deviation o., and the angle of the prism a from each tracing of procedure step 5. Calculate the index of refraction for the Lucite prism from these angles. 4. Find the average (mean) value for the index of refraction of the prism. 5. Calculate the velocity of light in the prism.Index of Refraction n= (6.2) Here c= 3 X 10 m/s, the speed of light in a vacuum, and / is the speed of light in the medium. For air to a very good approximation / = 1. The critical angle is the angle of incidence at which light begins to reflect, rather than refract, when it enters a new medium that has a lower index of refraction. This happens when the angle of refraction reaches 90. Substituting 02 = 90 in equation 6.1 and solving for 0, calculates the critical angle as shown in equation 6.3. Critical Angle 0, = sin ( 6.3) A prism is a transparent medium composed of two non-parallel polished surfaces. When light travels through a prism such that it enters one side and exits another, the total deviation 8, in the ray leaving the second side from the original angle of incidence is dependent on the index of refraction, n, and the angle between the two side of the prism a, as shown in figure 6.2. Original direction of the ray - Normal Normal B 01 Deviated direction of the ray Incident Ray Figure 6.2 Total deviation of a light ray through a prism The value of o depends on the angle of incidence of the light, 0,, at the first face of the prism. When the light passes symmetrically through the prism so that the angle of refraction at the second face is equal to angle of incidence at the first face, 0.= 0., then o has a minimum value o. If the light enters the prism from a near vacuum medium, for example air with an index of refraction of 1.00, then the index of refraction is calculable in terms of the angle between the two sides of the prism a and the total deviation o, as shown in equation 6.4. sin om + a Index of Refraction n a (6.4) sinACCEPTED VALUES The accepted value for the index of refraction for Lucite is 1.50. APPARATUS Straight filament lamp protractor Lucite prism ruler PROCEDURE 1. Place a sheet of blank paper on your desk. Arrange the light source and prism so that a narrow beam of light is incident on the prism as shown in figure 6.3. Figure 6.3 Trace of a light ray refracting at two surfaces. 2. Adjust the prism so that the angle of incidence on the first surface is between 450 and 60. Using two dots made with a sharp pencil to determine the direction of a straight line, trace the outline of the prism and the ray of light onto the paper. 3. Repeat steps 1 and 2 with a second surface with an angle of incidence greater than 60. 4 . Arrange the prism and the beam of light as in figure 6:4 so that the angle of refraction at the second surface is 90. Trace, as in step 2, the outline of the prism and the ray of light. A D Figure 6.4 Trace of a light ray refracting and then reflecting internally 5. Arrange the prism and the beam of light as in figure 6.5. Rotate the prism until the angle of deviation dis a minimum and then trace the outline of the prism and the beam of light. Repeat, using the other angle of the prism which is less than 90 as the refracting angle