Question: Hello, Below attached is a statistics lesson. Please solve when possible. Answer will be rated immediately. Thank you so much. Now, to determine how well
Hello,
Below attached is a statistics lesson. Please solve when possible. Answer will be rated immediately. Thank you so much.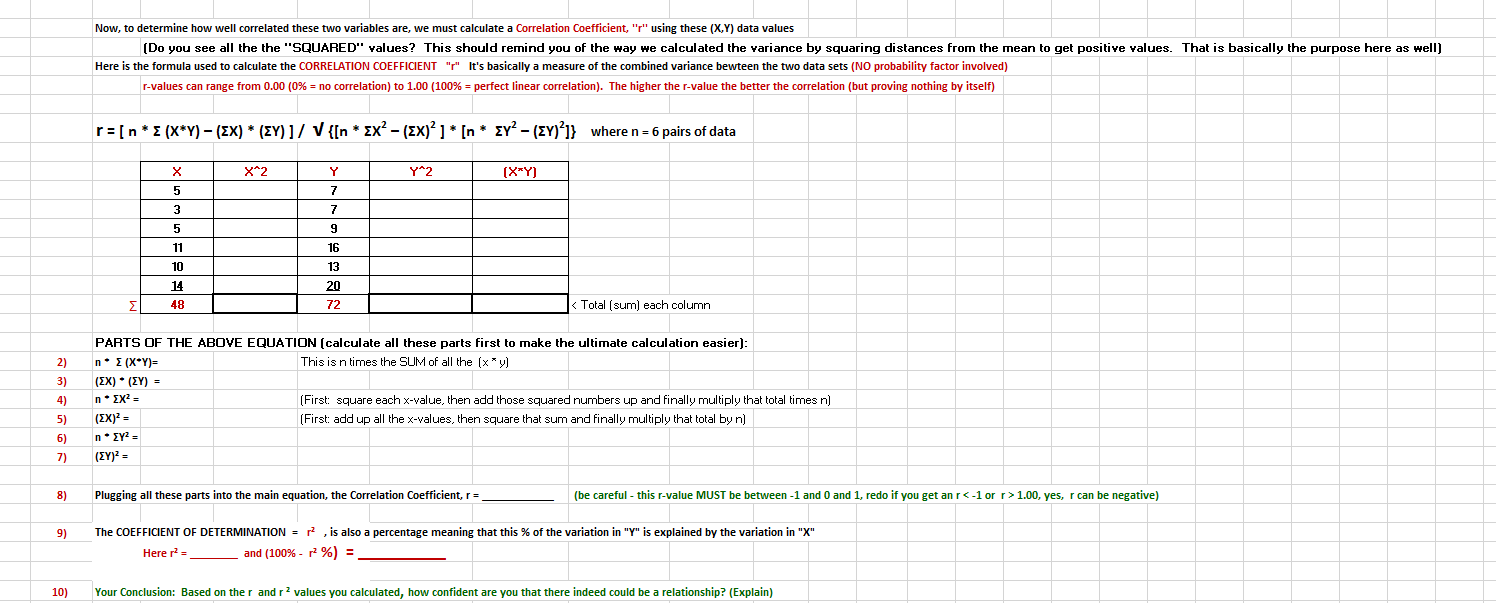
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


