Hello, can you help me write a matlab code for the given question??

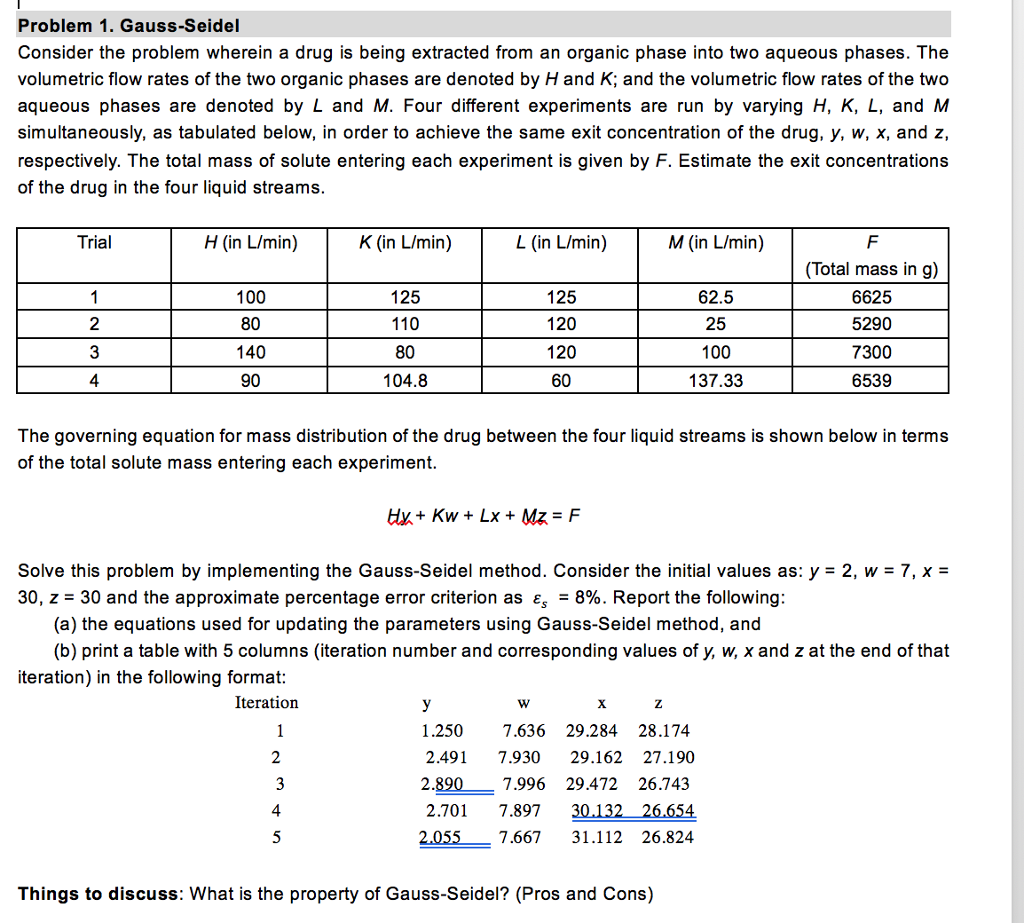
Problem 1. Gauss-Seidel Consider the problem wherein a drug is being extracted from an organic phase into two aqueous phases. The volumetric flow rates of the two organic phases are denoted by H and K; and the volumetric flow rates of the two aqueous phases are denoted by L and M. Four different experiments are run by varying H, K, L, and M simultaneously, as tabulated below, in order to achieve the same exit concentration of the drug, y, w, x, and z, respectively. The total mass of solute entering each experiment is given by F. Estimate the exit concentrations of the drug in the four liquid streams Trial H (in L/min) K (in L/min) L (in L/min) M (in L/min) 100 80 140 90 125 110 80 104.8 125 120 120 60 62.5 25 100 137.33 Total mass in g) 6625 5290 7300 6539 2 3 The governing equation for mass distribution of the drug between the four liquid streams is shown below in terms of the total solute mass entering each experiment Solve this problem by implementing the Gauss-Seidel method. Consider the initial values as: y= 2, w = 7, x = 30, z = 30 and the approximate percentage error criterion as = 8%. Report the following (a) the equations used for updating the parameters using Gauss-Seidel method, and (b) print a table with 5 columns (iteration number and corresponding values of y, w, x and z at the end of that iteration) in the following format Iteration 1.2507.636 29.284 28.174 2.4917.930 29.162 27.190 7.996 29.472 26.743 2.7017.89730132 26.654 7.66731.112 26.824 2 4 Things to discuss: What is the property of Gauss-Seidel? (Pros and Cons) Problem 1. Gauss-Seidel Consider the problem wherein a drug is being extracted from an organic phase into two aqueous phases. The volumetric flow rates of the two organic phases are denoted by H and K; and the volumetric flow rates of the two aqueous phases are denoted by L and M. Four different experiments are run by varying H, K, L, and M simultaneously, as tabulated below, in order to achieve the same exit concentration of the drug, y, w, x, and z, respectively. The total mass of solute entering each experiment is given by F. Estimate the exit concentrations of the drug in the four liquid streams Trial H (in L/min) K (in L/min) L (in L/min) M (in L/min) 100 80 140 90 125 110 80 104.8 125 120 120 60 62.5 25 100 137.33 Total mass in g) 6625 5290 7300 6539 2 3 The governing equation for mass distribution of the drug between the four liquid streams is shown below in terms of the total solute mass entering each experiment Solve this problem by implementing the Gauss-Seidel method. Consider the initial values as: y= 2, w = 7, x = 30, z = 30 and the approximate percentage error criterion as = 8%. Report the following (a) the equations used for updating the parameters using Gauss-Seidel method, and (b) print a table with 5 columns (iteration number and corresponding values of y, w, x and z at the end of that iteration) in the following format Iteration 1.2507.636 29.284 28.174 2.4917.930 29.162 27.190 7.996 29.472 26.743 2.7017.89730132 26.654 7.66731.112 26.824 2 4 Things to discuss: What is the property of Gauss-Seidel? (Pros and Cons)