Hello,

Could someone please explain me this how to calculate Accumulated Cash Flow Discounted and how the Future value of Project Cash Flow was calculated?

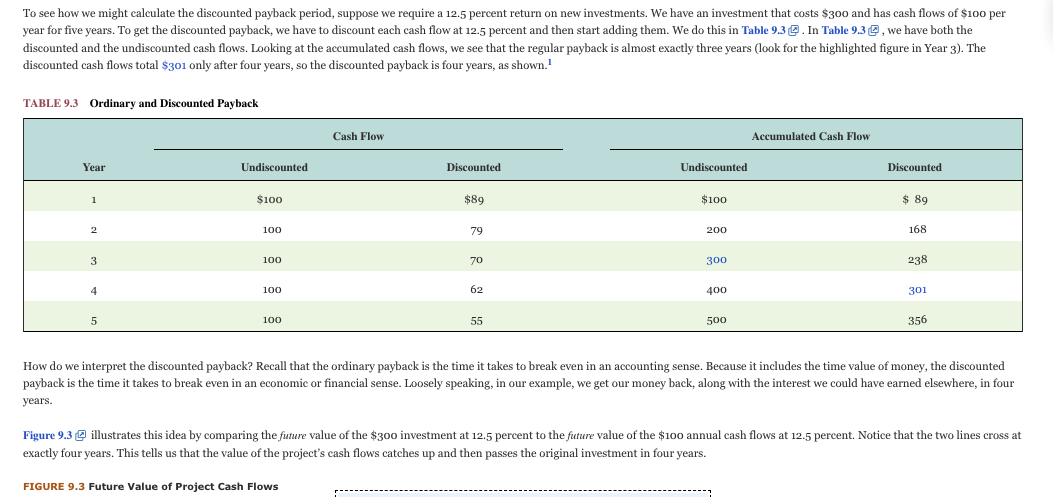
Table 9.3 Ordinary and Discounted Payback

And

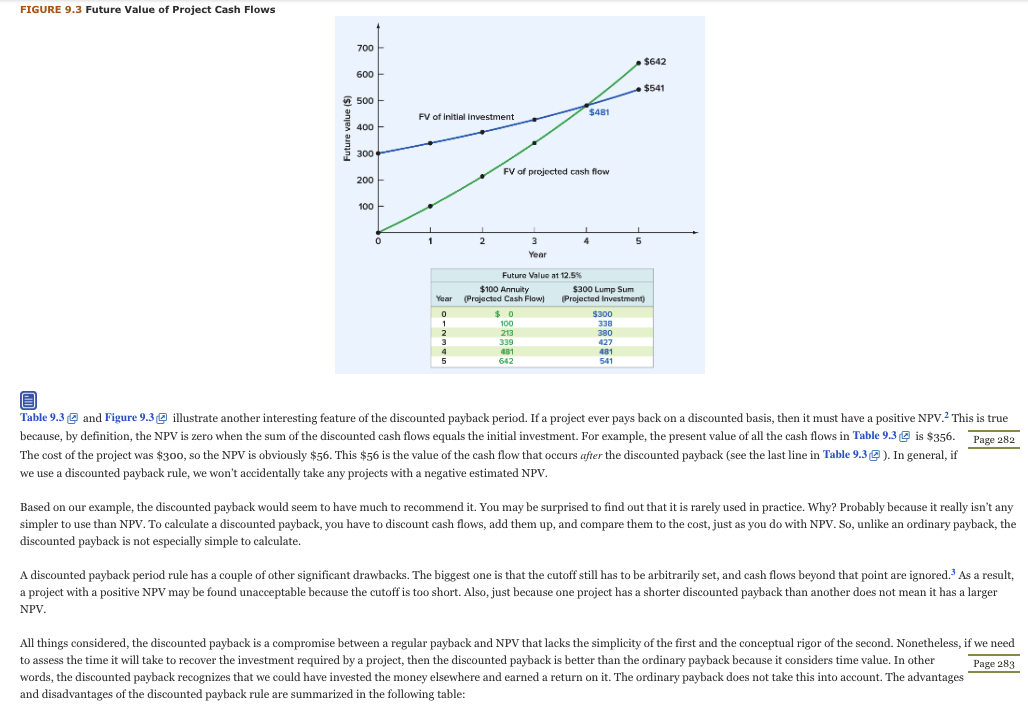
9.3 Future Value of Project Cash Flows

Thanks.

To see how we might calculate the discounted payback period, suppose we require a 12.5 percent return on new investments. We have an investment that costs $300 and has cash flows of $100 per year for five years. To get the discounted payback, we have to discount each cash flow at 12.5 percent and then start adding them. We do this in Table 9.3 . In Table 9.3, we have both the discounted and the undiscounted cash flows. Looking at the accumulated cash flows, we see that the regular payback is almost exactly three years (look for the highlighted figure in Year 3). The discounted cash flows total $301 only after four years, so the discounted payback is four years, as shown. TABLE 9.3 Ordinary and Discounted Payback Cash Flow Accumulated Cash Flow Year Undiscounted Discounted Undiscounted Discounted 1 $100 $89 $100 $ 89 2 100 79 200 168 3 100 70 300 238 4 100 62 400 301 5 100 55 500 356 How do we interpret the discounted payback? Recall that the ordinary payback is the time it takes to break even in an accounting sense. Because it includes the time value of money, the discounted payback is the time it takes to break even in an economic or financial sense. Loosely speaking, in our example, we get our money back, along with the interest we could have earned elsewhere, in four years. Figure 9.3 @ illustrates this idea by comparing the future value of the $300 investment at 12.5 percent to the future value of the $100 annual cash flows at 12.5 percent. Notice that the two lines cross at exactly four years. This tells us that the value of the project's cash flows catches up and then passes the original investment in four years. FIGURE 9.3 Future Value of Project Cash Flows FIGURE 9.3 Future Value of Project Cash Flows 700 $642 600 $541 500 PV of Initial investment 5481 400 300 FV of projected cash flow 200 100 1 0 2 4 5 3 Year Future Value at 12.5% $100 Annuity $300 Lump Sum Year (Projected Cash Flow Projected Investment) 0 $ 0 $300 1 1 100 338 2 2 213 380 3 339 427 4 481 481 5 642 541 Table 9.3 and Figure 9.3@illustrate another interesting feature of the discounted payback period. If a project ever pays back on a discounted basis, then it must have a positive NPV.? This is true because, by definition, the NPV is zero when the sum of the discounted cash flows equals the initial investment. For example, the present value of all the cash flows in Table 9.3 is $356. Page 282 The cost of the project was $300, so the NPV is obviously $56. This $56 is the value of the cash flow that occurs after the discounted payback (see the last line in Table 9.32 ). In general, if we use a discounted payback rule, we won't accidentally take any projects with a negative estimated NPV. Based on our example, the discounted payback would seem to have much to recommend it. You may be surprised to find out that it is rarely used in practice. Why? Probably because it really isn't any simpler to use than NPV. To calculate a discounted payback, you have to discount cash flows, add them up, and compare them to the cost, just as you do with NPV. So, unlike an ordinary payback, the discounted payback is not especially simple to calculate. A discounted payback period rule has a couple of other significant drawbacks. The biggest one is that the cutoff still has to be arbitrarily set, and cash flows beyond that point are ignored. As a result, a project with a positive NPV may be found unacceptable because the cutoff is too short. Also, just because one project has a shorter discounted payback than another does not mean it has a larger NPV. . All things considered, the discounted payback is a compromise between a regular payback and NPV that lacks the simplicity of the first and the conceptual rigor of the second. Nonetheless, if we need to assess the time it will take to recover the investment required by a project, then the discounted payback is better than the ordinary payback because it considers time value. In other Page 283 words, the discounted payback recognizes that we could have invested the money elsewhere and earned a return on it. The ordinary payback does not take this into account. The advantages and disadvantages of the discounted payback rule are summarized in the following table