hello, Dynamic programming question

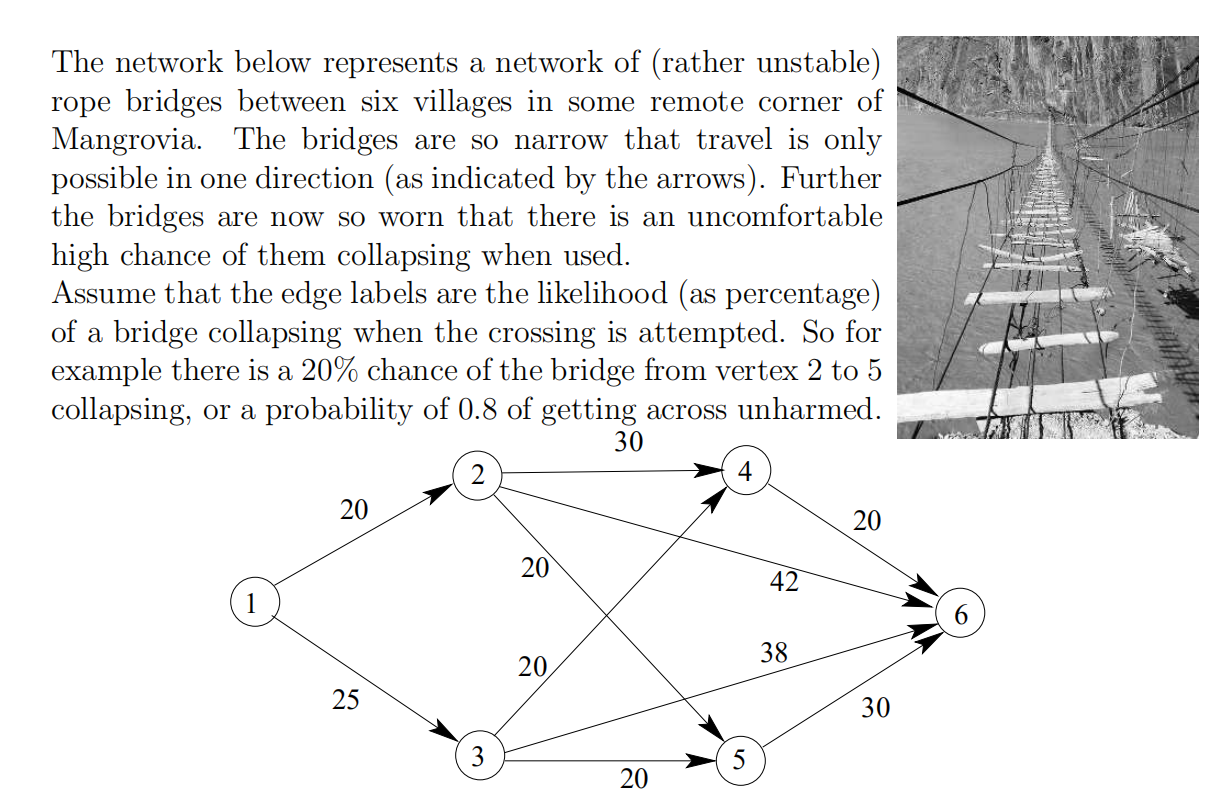
The network below represents a network of (rather unstable) rope bridges between six villages in some remote corner of Mangrovia. The bridges are so narrow that travel is only possible in one direction (as indicated by the arrows). Further the bridges are now so worn that there is an uncomfortable high chance of them collapsing when used. Assume that the edge labels are the likelihood (as percentage) of a bridge collapsing when the crossing is attempted. So for example there is a 20% chance of the bridge from vertex 2 to 5 collapsing, or a probability of 0.8 of getting across unharmed. The aim is to nd a path from vertex 1 to 6 which maximizes the probability of getting to vertex 6 alive. [Do all calculations of probabilities below to 4 decimal places] 1. Find the probability of survival for each leg in the network and draw the network with these probabilities shown. [2] . What is the probability of surviving a journey from 1 to 6 along legs (1,2), (2,5) and (5,6)? [2] . Prove that for this problem the Principle of Optimality holds: (i.e. \"The optimal path from any node to the end does not depend on how you arrived at that node\" * adapt the three line proof given in the lecture for the shortest/ longest path to this case) and derive a DP recurrence for for this problem. [6] . Showing your working on the diagram, solve the problem by DP to nd the safest route from 1 to 6. [4] . Repeat the calculation in a table form. [5]