Hello! I have a question regarding following Kernal problems. Thank you in advance..!

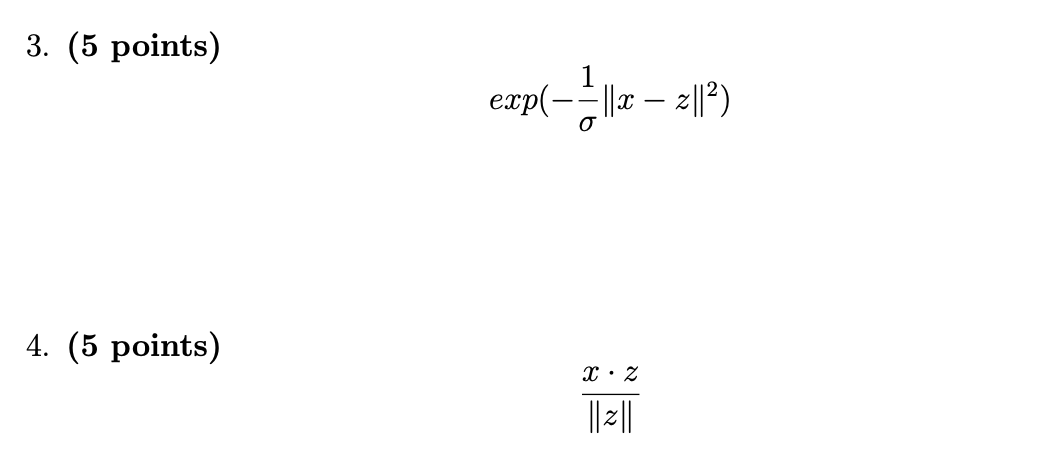
A necessary and suicient condition of a kernel is that the resulting Gram matrix be positive semidenite. In practice that is difcult to prove. Another method is to show that the proposed kernel function can be decomposed into the dot product between two points in some transformed feature space, e.g., k(a:, z) = (Mat) - (15(2). Again, this decomposition is too cumbersome. An easier technique is to demonstrate that your kernel is composed of simpler kernels according to kernel construction techniques (see a nonexhaustive list below). For a complete list see PRML chapter 6 section 2. Mm, z) = ck1(93, 2) [6(1', 2) = k1(.:r, z) | k2(:c, z) (23, Z) = f($)k1($, Z)f(z) ( ( ( 23'3" x, z) = emp(k1(x, 2)) k "3: Z) = k1(f($).f(2)) k 2:, z) = q(k1(x,z)) Figure 1: Kernel construction techniques. f (-) is any function. c is a scalar. q(-) is a polynomial with nonnegative coefcients. kit, -) is a kernel function. For each of the functions below, prove Whether or not it is a valid kernel. Here a: and z are two column vectors. Hint: remember that kernels are symmetric: Mrs, 25) = k(z,x). 1. (5 points) ( )2 2. (5 points) (m - z + 1)2