hello! i have done the assignment but it is a bit incorrect.. my teacher gave me feedback and i would like help on putting all of the feedback into my assignment so that i could get a good grade.

My assignment:

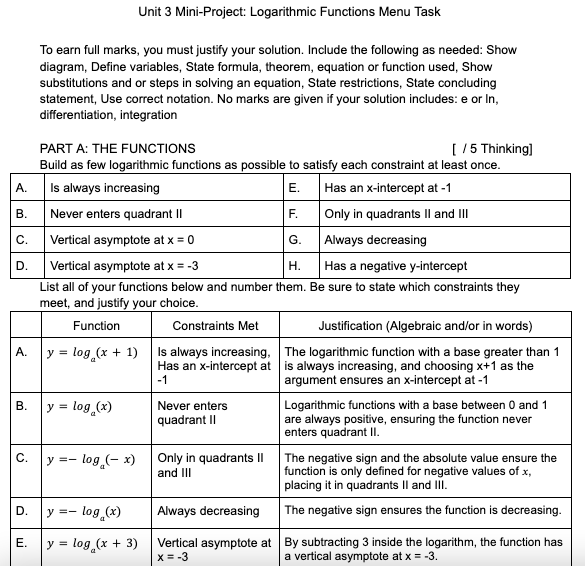
Unit 3 Mini-Project: Logarithmic Functions Menu Task To earn full marks, you must justify your solution. Include the following as needed: Show diagram, Define variables, State formula, theorem, equation or function used, Show substitutions and or steps in solving an equation, State restrictions, State concluding statement, Use correct notation. No marks are given if your solution includes: e or In, differentiation, integration PART A: THE FUNCTIONS [ / 5 Thinking] Build as few logarithmic functions as possible to satisfy each constraint at least once A. Is always increasing E. Has an x-intercept at -1 B Never enters quadrant II F. Only in quadrants II and Ill C Vertical asymptote at x = 0 3 Always decreasing D Vertical asymptote at x = -3 H. Has a negative y-intercept List all of your functions below and number them. Be sure to state which constraints they meet, and justify your choice. Function Constraints Met Justification (Algebraic and/or in words) A. y = log (x + 1) Is always increasing, The logarithmic function with a base greater than 1 Has an x-intercept at is always increasing, and choosing x+1 as the -1 argument ensures an x-intercept at -1 B. y = log (x) Never enters Logarithmic functions with a base between 0 and 1 quadrant Il are always positive, ensuring the function never enters quadrant II. C. y =- log (- x) Only in quadrants II The negative sign and the absolute value ensure the and Ill function is only defined for negative values of x, placing it in quadrants II and Ill. D. y =- log (x) Always decreasing The negative sign ensures the function is decreasing. E. y = log (x + 3) Vertical asymptote at By subtracting 3 inside the logarithm, the function has X=-3 a vertical asymptote at x = -3.E. y = log (x + 3) Vertical asymptote at | By subtracting 3 inside the logarithm, the function has X =-3 a vertical asymptote at x = -3. F. y =- log (x + 1) Has a negative The negative sign ensures a negative y-intercept. y-intercept Unit 3 Mini-Project: Logarithmic Functions Menu Task PART B: DISCUSSION [ /5 Communication] Answer the following in complete sentences. Give full and complete explanations. Which constraints group nicely? The constraints A, C, and G make a good group. The logarithmic expressions for the functions subject to these constraints may have bases in common. Which constraints cannot be grouped? Certain conditions that are difficult to combine with others are involved in Constraints B, F, D, and H. They need different functions.PART B: DISCUSSION [ /5 Communication] Answer the following in complete sentences. Give full and complete explanations. Which consltraints group nicely? - The constraints A, C, and G make a good group. The logarithmic expressions for the functions subject to these constraints may have bases in common. Which consltraints cannot be grouped? - Certain conditions that are difficult to combine with others are involved in Constraints B, F. D, and H. They need different functions. Is it possible to solve in exactly 2 logarithmic functions? 37 47 - Using just two logarithmic functions to satisfy all constraints is difficult. Asymplotes, intercepts, and quadrant restrictions are among the constraints that are often indicated for different functions. - Still, this might be possible if three or more logarithmic functions are used. - Looking al constraints on possible groups or parts: - Always increasing with a -1 x-intercept: It is possible to group these restrictions together. For instance, the logarithmic function y = log (x + 1) salisfies both. - The function meets constraints A, B, and Fl