Hello. Please help me solve these questions

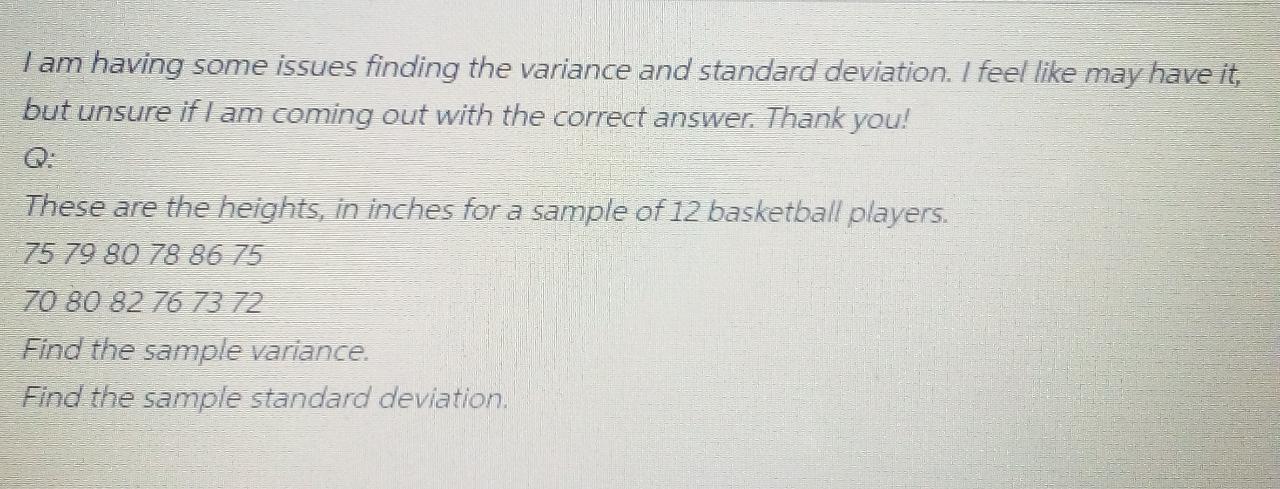
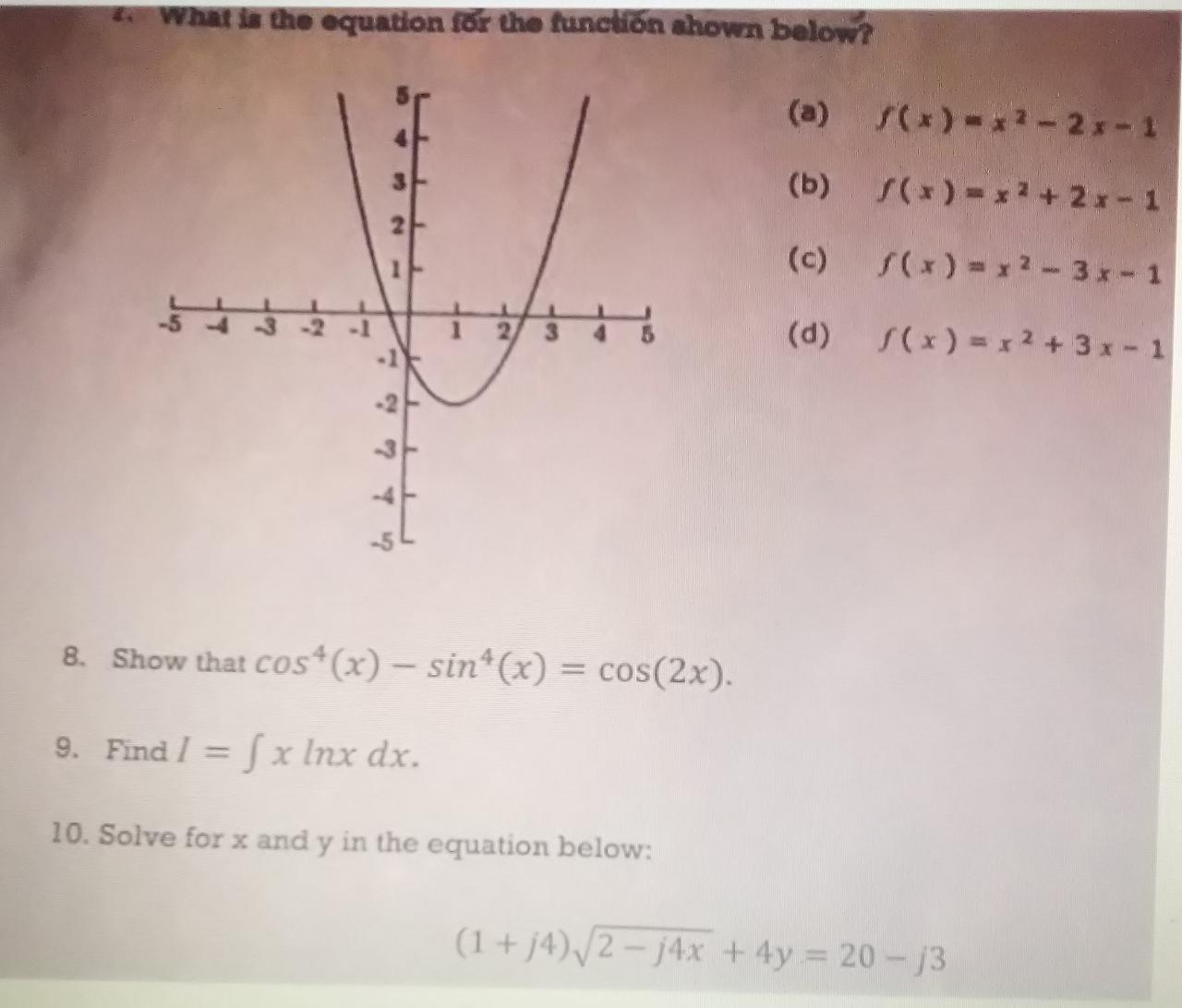
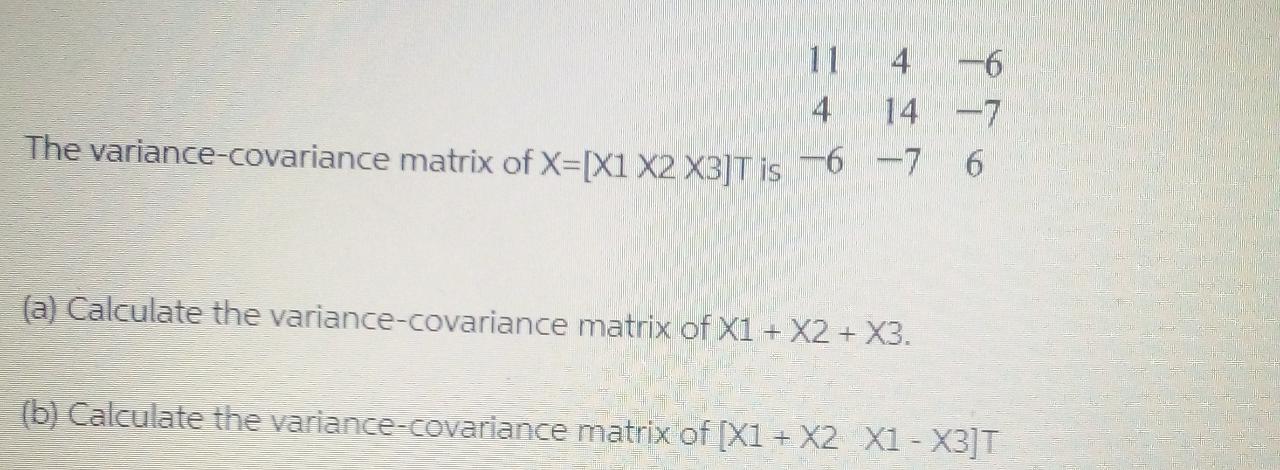
I am having some issues finding the variance and standard deviation. I feel like may have it, but unsure if I am coming out with the correct answer. Thank you! Q: These are the heights, in inches for a sample of 12 basketball players. 75 79 80 78 86 75 70 80 82 76 73 72 Find the sample variance. Find the sample standard deviation.What is the equation for the function shown below? (a) f(x) -x2-2x-1 (b ) / ( x ) = x2+2x- 1 2 (c) 5 (x ) = x2 - 3x-1 - 5 -2 2 (d) S ( x) = x2+3x -1 in to do is 8. Show that cost(x) - sint (x) = cos(2x). 9. Find I = [ x Inx dx. 10. Solve for x and y in the equation below: (1 + /4) 2 -j4x + 4y = 20-13n the multiple regression model ynx1=Xnx(k+1) B(k+1)x1+unx1,ynx1=Xnx(k+1) B(k+1)x1+unx1, where the first column of XX is a vector of ones and the columns of XX are linearly independent. Which one of the following statements is not an implication of E(ulX)=OE(ulX)=0? Select one: a. E((X'X)-1X'u)=OE((XX)-1X'u)=0 b. E(yIX)=XBE(yIX)=XB C. Var(ulX)=02InVar(u|X)=2In where Inin is an nxnnxn identity matrix. d. B"BA, the OLS estimator of BB, is an unbiased estimator of BB e E(X'u)=0\f1. (30) In this problem you will find out how to calculate PRESS residuals from the results of a single least square fit using all observations. There is another proof in Appendix C.7 of the textbook using the Sherman-Morrison-Woodbury formula. The arguments here are more intuitive and geometric. Suppose we have data (x,, vi). .... (X,., y.). If we fit the regression model yi = XB+6, 1sign. and use 3 to denote the least square estimate, then the usual i-th residual is defined as er = yi - Ji = UI - XiB (b) Suppose we have the data X1 0). .... (X, 1, 0). (X.(). (X1. 0). . (x0) (2) Show that if we fit the regression model using data in (2), then the i-th residual is I - halem , where he is the i-th diagonal entry of the hat matrixShort Run and Long Run Cost Function We consider the same production function is X=F(K,L)=3K^1/3L^1/3. Define the wage cost as w and the rental rate of capital as r. The price of the product is defined as p. 1. Consider a short run case where the amount of capital is fixed at K = K " . In this case, the short run firm cost is wL + rk . The firm produces output x using K - and L. Calculate the demand for labor input L for output x in the short run. 2. The cost function explains the relationship between total cost C and the firm output x. Solve for the short run cost function (where K - is fixed) by substituting L into the firm cost expression. 1 3. From the short run cost function solved in the previous question, we consider the short run firm profit maximization problem: given market price of production p and factor prices (w, r), the firm maximizes its profit by choosing the output of production x. Solving this short-run profit maximization problem, and derive the short run supply curve. 4. In the long run, the usage of capital can be changed as well. Thus, the long run firm cost is who rk. For a firm producing output x with k and L, calculate the new cost- minimizing usage of inputs K. and L. 5. Solve for the long run cost function (where K is flexible) by substituting K and L in question 4 into the long-run cost expression: 6, Solve the firm profit maximization problem in the long run and derive the long run supply curve