Hello, PLEASE ONLY SOLVE QUESTION 2! Thank you!

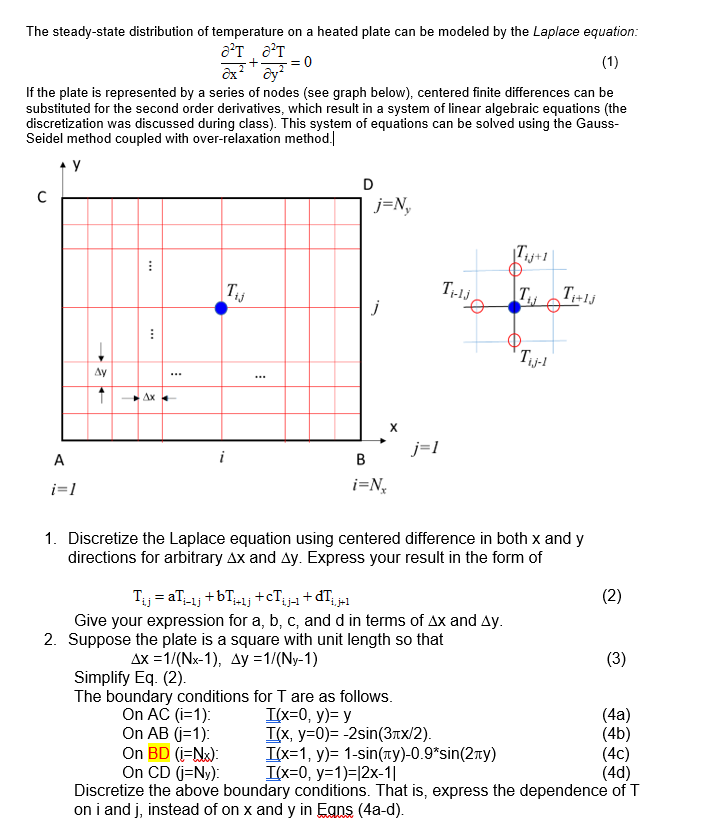
The steady-state distribution of temperature on a heated plate can be modeled by the Laplace equation: at O'T + = 0 (1) Oxy? If the plate is represented by a series of nodes (see graph below), centered finite differences can be substituted for the second order derivatives, which result in a system of linear algebraic equations (the discretization was discussed during class). This system of equations can be solved using the Gauss- Seidel method coupled with over-relaxation method. Y D j=N, : Ti Tolig Ti+lj Tj j : T-1 Ay ... 1 AX j=1 A A B i=N, i=1 1. Discretize the Laplace equation using centered difference in both x and y directions for arbitrary Ax and Ay. Express your result in the form of ;+cTija + dT j-2 (2) 7 (3) Tij = aT.-2; +BT:+2) Give your expression for a, b, c, and d in terms of Ax and Ay. 2. Suppose the plate is a square with unit length so that Ax =1/(Nx-1), Ay = 1/(Ny-1) (3) Simplify Eq. (2). The boundary conditions for T are as follows. On AC (i=1): (x=0, y)= y (4a) On AB (j=1) T(x, y=0)= -2sin(31x/2). (45) On BD (i=Nx): Ifx=1, y)= 1-sin(ny)-0.9*sin(2ny) (40) On CD (j=Ny): I(x=0, y=1)=2x-11 (40) Discretize the above boundary conditions. That is, express the dependence of T on i and j, instead of on x and y in Egns (4a-d)