Hello, Seeking guidance to help double check my answer on this homework lab question. Any reply is greatly appreciated, Full walkthrough is not needed.

Thank you!

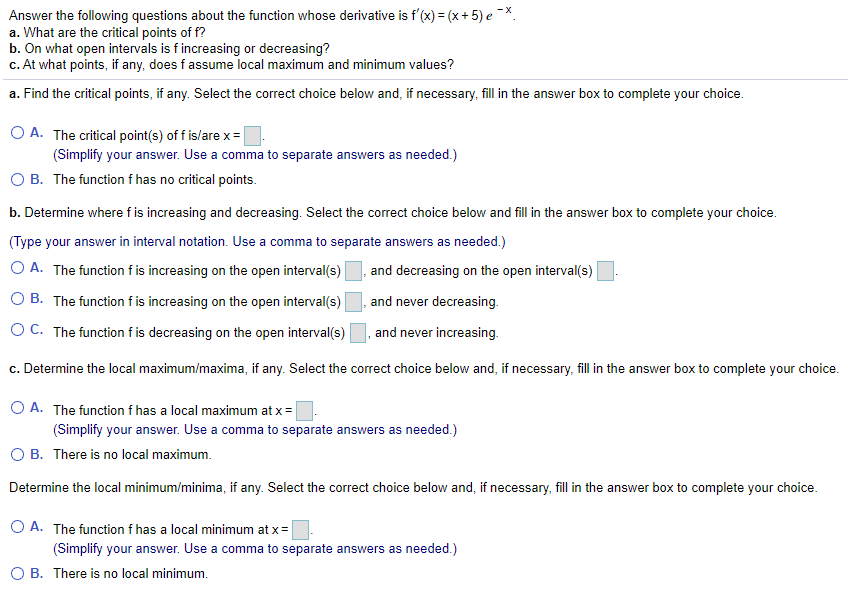
Answer the following questions about the function whose derivative is f'(x) = (x + 5) e -*. a. What are the critical points of f? b. On what open intervals is f increasing or decreasing? c. At what points, if any, does f assume local maximum and minimum values? a. Find the critical points, if any. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The critical point(s) of fis/are x = (Simplify your answer. Use a comma to separate answers as needed.) O B. The function f has no critical points. b. Determine where f is increasing and decreasing. Select the correct choice below and fill in the answer box to complete your choice. (Type your answer in interval notation. Use a comma to separate answers as needed.) O A. The function f is increasing on the open interval(s) , and decreasing on the open interval(s) O B. The function f is increasing on the open interval(s) , and never decreasing. O C. The function f is decreasing on the open interval(s) , and never increasing. c. Determine the local maximum/maxima, if any. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The function f has a local maximum at x = (Simplify your answer. Use a comma to separate answers as needed.) O B. There is no local maximum. Determine the local minimum/minima, if any. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The function f has a local minimum at x = (Simplify your answer. Use a comma to separate answers as needed.) O B. There is no local minimum