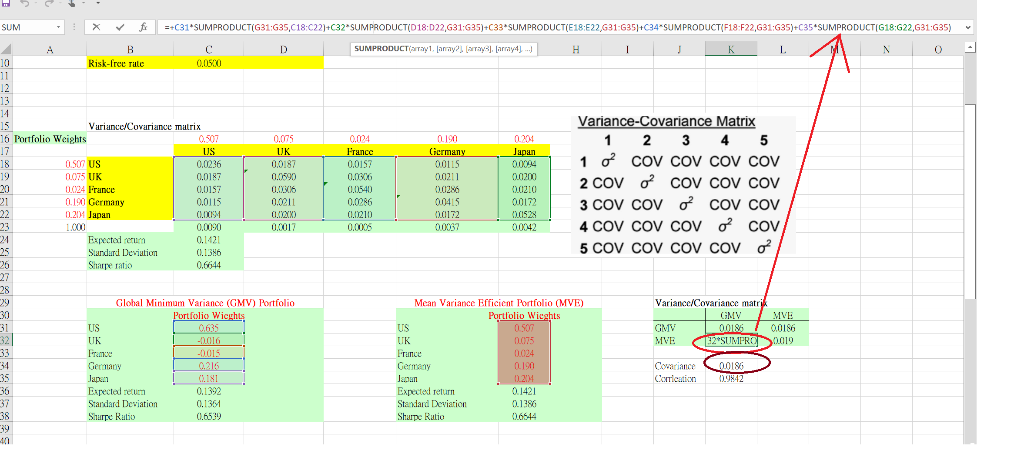
Question: Hello, the grey circle(K34) here has a cell value equals to the one of the red circle (K32), and the display show the formula of

Hello, the grey circle(K34) here has a cell value equals to the one of the red circle (K32), and the display show the formula of cell K32.

May I know what is the meaning of the formula, is there any equation for it? Why is it the calculation of covariance (grey circle ,cell K34) is using that formula?

As I know, equation of covariance : C o v ( X , Y ) = ( X i X ) ( Y i Y ) n , and there should be average of values x and y. But here there isn't any average values given in this set of data, how could covariance be calculated in the way expressed in the excel worksheet?

Thank you.

Hello, the grey circle(K34) here has a cell value equals to the

SUM - .fi =+C31 SUMPRODUCT(G31:435,C18:C22]+C32*SUM PRODUCT(D18:022,631:435)+C33 SUMPRODUCT(E18:E22,G31-G351+C34-SUMPRODUCT/F18:F22,G31:G35)+C35 SUMPRODUCT[G18:G22,631:35) SUMPRODUCT Aray(array(array) ... H 1 L 0 1204 Japan 0.004 France 0,0157 0.06% 0.0540 0.0286 0.01210 0.0005 0.190 Ciermany 00115 00211 00286 000415 0200172 0.0087 00200 00210 00172 0528 00042 B D 10 Risk-Tree Tule 0.00 11 12 13 14 15 Variancc/Covuriance mutrix 16 Portfolio Weights 0.507 0.005 17 US UK 18 OSOT US 0.0236 19 0.075 UK 0.0187 0.0590 20 0.024 France 0.0157 0.XXSC6 21 0.190 Germany 0.0115 0.0211 0.214 Japan 0.001 OLMAK) 23 1.000 0.0090 0.0012 24 Expectedre 0.1421 25 Standard Deviation 0.130 26 Sharpe ratio 0.6644 27 28 29 Global Minimum Variance (GMV) Portfolio 30 Portfolio Wicghts 31 US 32 UK -2016 33 France -0.015 34 Germany 0.216 35 Japan 0.181 36 Expected en 0.1392 37 Standard Deviation 0.1351 38 Sharpe Ratio 0.6539 19 41 Variance-Covariance Matrix 1 2 3 4 5 1 oCOV COV COV COV 2 COVO? COV COV COV 3 COV COVO?COV COV 4 COV COV COVCOV 5 COV COV COV COV? Variance/Covariance matri GMV MVE GMV 0019 00186 MVE 132 SUMPRC0019 Mean Variance Efficient Portfolio (MVE) Portfolio Wichts US 0.500 UK 0073 France 0024 Germany 0.190 Japan 0.2014 Expected return 0.1421 Standard Deviation 0.13 Shape Ratio 0.6544 Cowariance Carication 2018 09842 SUM - .fi =+C31 SUMPRODUCT(G31:435,C18:C22]+C32*SUM PRODUCT(D18:022,631:435)+C33 SUMPRODUCT(E18:E22,G31-G351+C34-SUMPRODUCT/F18:F22,G31:G35)+C35 SUMPRODUCT[G18:G22,631:35) SUMPRODUCT Aray(array(array) ... H 1 L 0 1204 Japan 0.004 France 0,0157 0.06% 0.0540 0.0286 0.01210 0.0005 0.190 Ciermany 00115 00211 00286 000415 0200172 0.0087 00200 00210 00172 0528 00042 B D 10 Risk-Tree Tule 0.00 11 12 13 14 15 Variancc/Covuriance mutrix 16 Portfolio Weights 0.507 0.005 17 US UK 18 OSOT US 0.0236 19 0.075 UK 0.0187 0.0590 20 0.024 France 0.0157 0.XXSC6 21 0.190 Germany 0.0115 0.0211 0.214 Japan 0.001 OLMAK) 23 1.000 0.0090 0.0012 24 Expectedre 0.1421 25 Standard Deviation 0.130 26 Sharpe ratio 0.6644 27 28 29 Global Minimum Variance (GMV) Portfolio 30 Portfolio Wicghts 31 US 32 UK -2016 33 France -0.015 34 Germany 0.216 35 Japan 0.181 36 Expected en 0.1392 37 Standard Deviation 0.1351 38 Sharpe Ratio 0.6539 19 41 Variance-Covariance Matrix 1 2 3 4 5 1 oCOV COV COV COV 2 COVO? COV COV COV 3 COV COVO?COV COV 4 COV COV COVCOV 5 COV COV COV COV? Variance/Covariance matri GMV MVE GMV 0019 00186 MVE 132 SUMPRC0019 Mean Variance Efficient Portfolio (MVE) Portfolio Wichts US 0.500 UK 0073 France 0024 Germany 0.190 Japan 0.2014 Expected return 0.1421 Standard Deviation 0.13 Shape Ratio 0.6544 Cowariance Carication 2018 09842

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Finance Questions!

12:38 4 Assignment Details MTH 154-N41A: Quantitative Reasoning (SP21) MTH 154 Excel Project In this major project, you will create an Excel file and answer questions about linear and exponential...

BA 1605: Midterm Recap (Due: Feb. 27, 2015) Name _____________________________ 50 Student ID _____________________________ Section 01B 10:00~11:20 am Section 02B 01:00~02:20 pm [Questions 4 ~ 7] The...

I have attached the discussion board 6 questions,scenario. and lectures for yourreview and response. I will submit a students questions for a response when I receive one. Thank You MKT500 Discussion...

I want to know how all the numbers are going and which ones are specific to organize them by cell 00 Estilos de celda v Formato y filtrar seleccionar datos G14 X V fx A B C D E F G H K L M N O Smith...

Please help me make this excel spreadsheet. It is for CSIS 100 class and I have no access to excel. Thank you for your time! I can plug my numbers and what not in I just don't have enough time with...

I do not understand any of this, and I wondered if anyone could explain it in simple terms? I am confused about how to do this, and my class ends in less than 24 hours. I uploaded everything from the...

pleass hslp ms on hos to complete this assignment with the steps i also attached Font 10 N Company Name Actual Expenses Sheet First Two Quarters of 2021 February June Trends May Total lan Percent of...

Scenario/Summary Hopefully you will find this week's iLab activity fun and useful. We'll be exploring the world of statistics from a business perspective this week, allowing you to practice your...

Could you please help me with the assignment? The instructions, marking rubric and statistics are in the folders. Thank you. ACC ACF 2400 - Semester 2, 2017 Individual Assignment 1: Building a...

The ratio of grade A officers and grade B officers is 3:7, and that of grade B and grade C officers is 2:5. If the total number of officers is 1375, then find the number of grade A officers? 1. 100...

What are the major accounts of the balance of payments, and what transactions are recorded on each account?

A company falled to record unrealized gains of $ 2 5 million on its debt investments classified as trading securities . Its tax rate is 2 5 % . As a result of this error, total shareholders' equity...

Name of the company PMO establishment option- current or existing Scalability Model Update on PMO set-up Specify the exact person(s) responsible for each specific task. Next action Team procedure or...

5. Which of the following are elements of current U.S. farm policy? LO22.5 a. Farmers are free to choose how much to plant of any particular crop. b. Direct payments. c. Price supports. d....

1. Suppose that corn currently costs $4 per bushel and that wheat currently costs $3 per bushel. Also assume that the price elasticity of corn is 0.10, while the price elasticity of wheat is 0.15....

3. Suppose that 10 workers were required in 2010 to produce 40,000 bushels of wheat on a 1,000-acre farm. LO22.2 a. What is the average output per acre? Per worker? b. If in 2020 only 8 workers...