Hello tutor. I need help for these problems

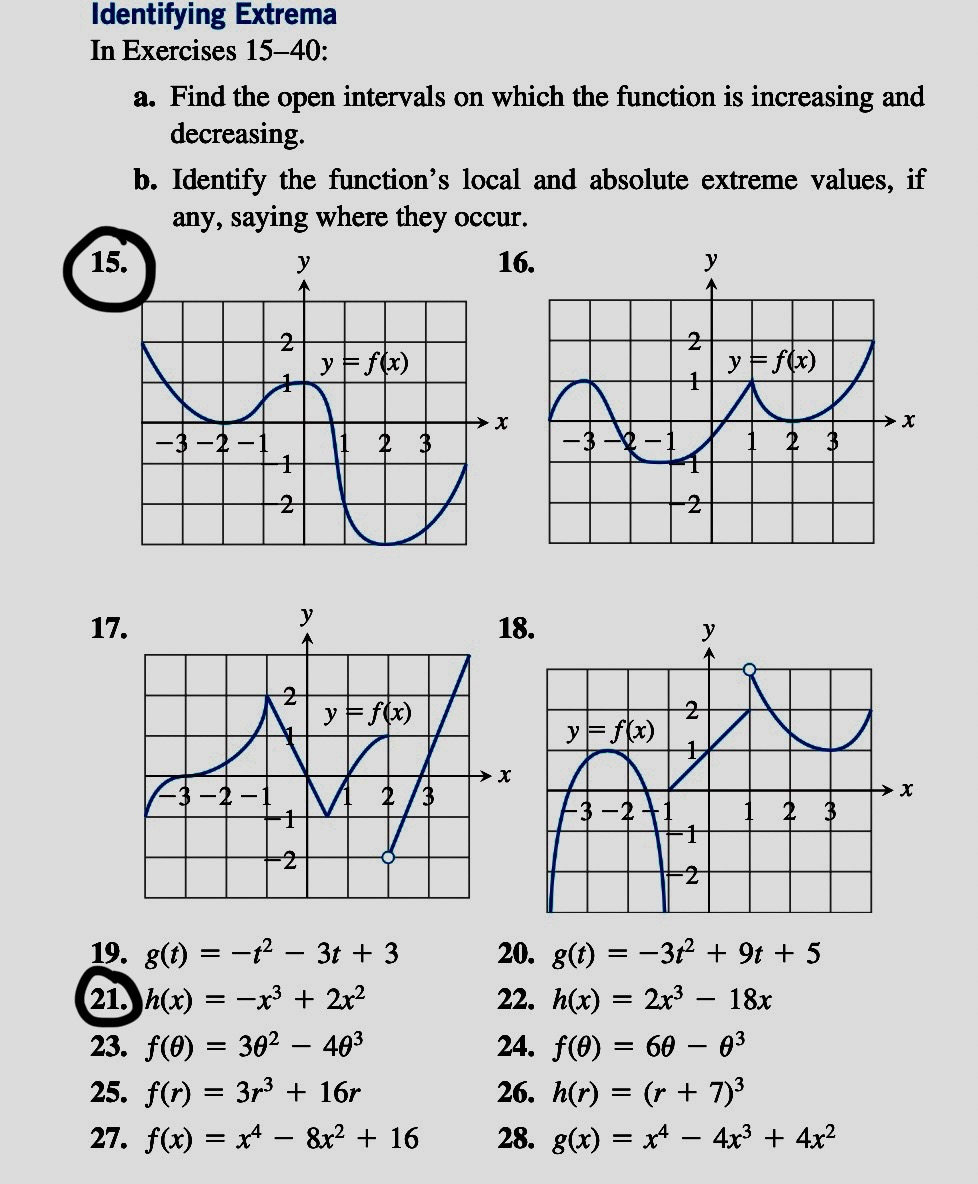
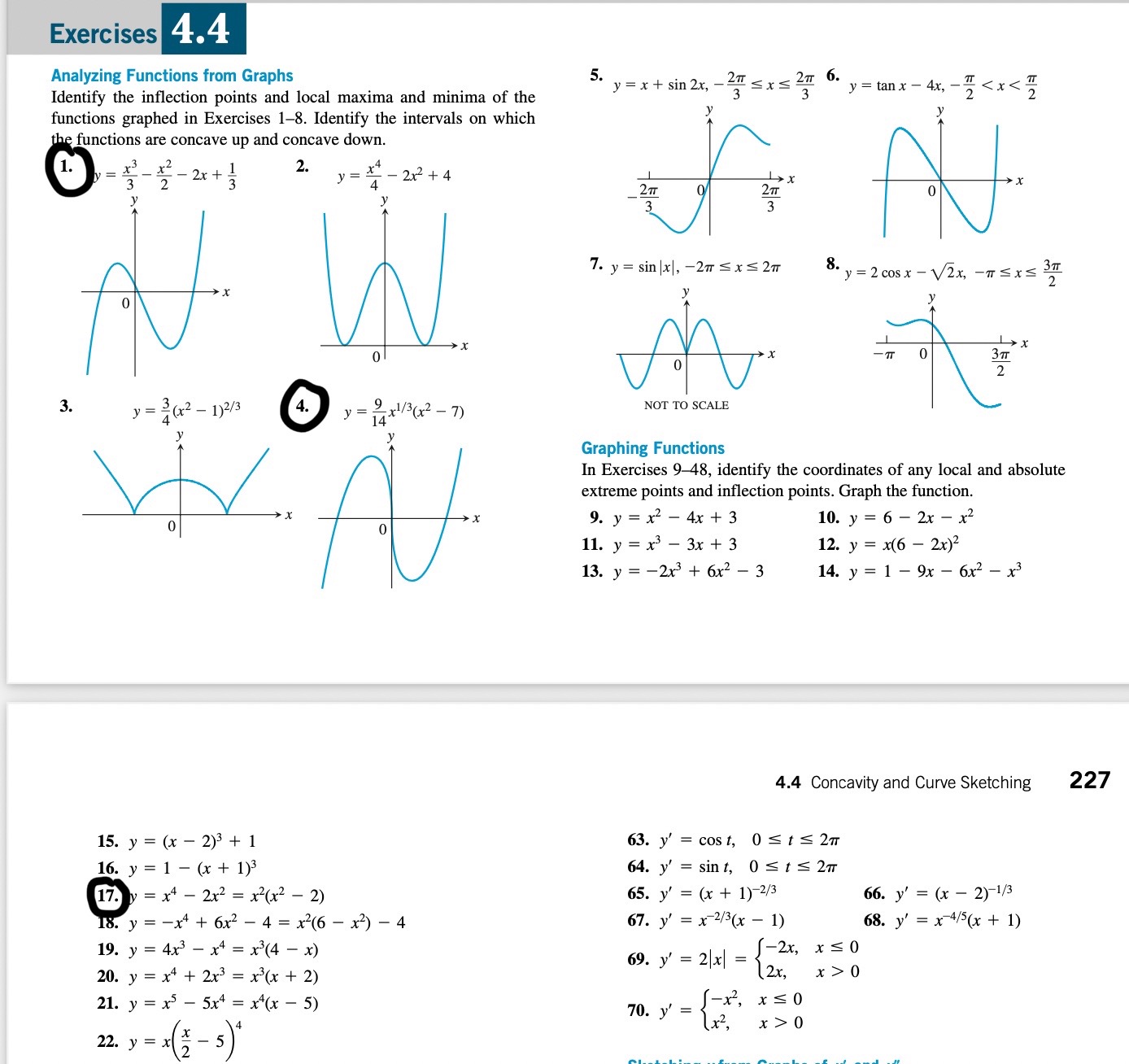
Exercises 3.9 Finding Linearizations X 12. f(x) =+ , a = 1.3 In Exercises 1-5, find the linearization L(x) of f(x) at x = a. 1. f(x) = x3 - 2x + 3, a = 2 13. Show that the linearization of f(x) = (1 + x)* at x = 0 is 2. f(x) = Vx2 + 9, a=-4 L(x) = 1 + kx. 14. Use the linear approximation (1 + x)* ~ 1 + kx to find an 3. f (x ) = x+ +, a=1 approximation for the function f(x) for values of x near zero. 4. f( x) = Vx, a = -8 a. f(x) = (1 - x)6 b. f(x) = 2 1 - x 5. f(x) = tan x, a = T 6. Common linear approximations at x = 0 Find the lineariza- c. f(x) = - 1 d. f(x) = V2+ x2 tions of the following functions at x = 0. V1+ x a. sin x b. cos x c. tan x e. f(x) = (4 + 3x) 1/3 f. f(x) = X 2+ x Linearization for Approximation In Exercises 7-12, find a linearization at a suitably chosen integer near 15. Faster than a calculator Use the approximation (1 + x)* ~ a at which the given function and its derivative are easy to evaluate. 1 + kx to estimate the following. 7. f(x) = x2 + 2x, a = 0.1 a. (1.0002)50 b. V1.009 8. f(x) = x, a =0.9 16. Find the linearization of f(x) = Vx + 1 + sin x at x = 0. How 9. f(x) = 2x2 + 3x - 3, a= -0.9 is it related to the individual linearizations of Vx + 1 and sin x at x = 0? 10. f(x) = 1 + x, a = 8.1 11. f (x) = Vx, a=8.5Exercises 4.1 Finding Extrema from Graphs 3. In Exercises 1-6, determine from the graph whether the function has any absolute extreme values on [a, b]. Then explain how your answer is consistent with . Theorem 1 1. 2. y = h(x) y = f(x) 0 X b 0 A a C2 a C b 6. y = g(x) y = g(x) X > X b b In Exercises 7-10, find the absolute extreme values and where they occur. 7. 8. X -2 0 2 9 . 10. (1, 2) N X - 3 -1 0 2Local Extrema and Critical Points In Exercises 5966, nd the critical points, domain endpoints, and extreme values (absolute and local) for each function. 59. y = x2530: + 2) 60. y = x2530; 4) 151.y=x'v'4x2 @y=x2V3x 63.y={42x' x51.={3x, Air-1 3+2xx2, x20 _ x22x+4, x51 65'y_{x2+6x4, x>1 12 1 15 _._. _...... +._._. 66y 4x 2x 4, x_l x36x2+8x, x>l In Exercises 67 and 68, give reasons for your answers. .Let f(x) = (x 2W3. a. Does f'(2) exist? I). Show that the only local extreme value of 3' occurs at x = 2. c. Does the result in part (b) contradict the Extreme Value Theorem? (1. Repeat parts (a) and (b) for f(x) = (x a)\Exercises m Checking the Mean Value Theorem Find the value or values of c that satisfy the equation f8?) n) _ , b _ a ' f (C) in the oonolusion of the Mean Value Theorem for the functions and intervals in Exercises 16. 90:) =x2+2x 1, [0,1] . x) = xz, [0,1] Identifying Extrema In Exercises 15-40: a. Find the open intervals on which the function is increasing and decreasing. b. Identify the function's local and absolute extreme values, if any, saying where they occur. 15. y 16. 2 y Ff( x) >X -3-2-1 2 3 17. 18. 2 y Ff( x) 2 y = f(x) >X -3-2-1 2 /3 -3 - 2 2 3 19. g(1) = -12 - 3t + 3 20. g(t) = -312 + 9t + 5 21. h(x) = -x3 + 2x2 22. h(x) = 2x3 - 18x 23. f(0) = 302 - 403 24. f(0) = 60 - 93 25. f(r) = 3r3 + 16r 26. h(r) = (r+ 7)3 27. f(x) = x4 - 8x2 + 16 28. g(x) = x4 - 4x3 + 4x2Exercises 4.4 Analyzing Functions from Graphs 5. y = x + sin 2x, -2" Exs 21 6. Identify the inflection points and local maxima and minima of the " y = tan x - 4x, - 7 functions graphed in Exercises 1-8. Identify the intervals on which he functions are concave up and concave down. 1. 5 -27 -2x+ } 2 . y = * - 212 + 4 > x 2 TT 7. y = sin |x|, -2T S xS 27 8. y = 2 cos x - V/2x, -TSXS 31 01 -TT 3 17 3. y = 3(x 4. 14 x 1/3 ( x 2 - 7 ) NOT TO SCALE y Graphing Functions In Exercises 9-48, identify the coordinates of any local and absolute extreme points and inflection points. Graph the function. 9. y = x2 - 4x + 3 10. y = 6 - 2x - x2 11. y = x3 - 3x + 3 12. y = x(6 - 2x)2 13. y = -2x3 + 6x2 - 3 14. y = 1 - 9x - 6x2 - x3 4.4 Concavity and Curve Sketching 227 15. y = (x - 2)3 + 1 63. y' = cost, O S t s 2T 16. y = 1 - (x + 1)3 64. y' = sint, Ost = 2n 17. y = x4 - 2x2 = x2(x2 - 2) 65. y' = (x + 1)-2/3 66. y' = (x - 2)-1/3 18. y = -x4 + 6x2 - 4 = x2(6 - x2) - 4 67. y' = x-2/3(x - 1) 68. y' = x 4/5(x + 1) 19. y = 4x3 - x4 = x3(4 - x) 69. y' = 2|x1 = J-2x, x50 20. y = x4 + 2x3 = x(x + 2) 2x, x 2 0 21. y = x5 - 5x4 = x*(x - 5) 70. y' = -x, x50 x >0 22. y = x(* - 5)