HELP! MATLAB PROBLEMS

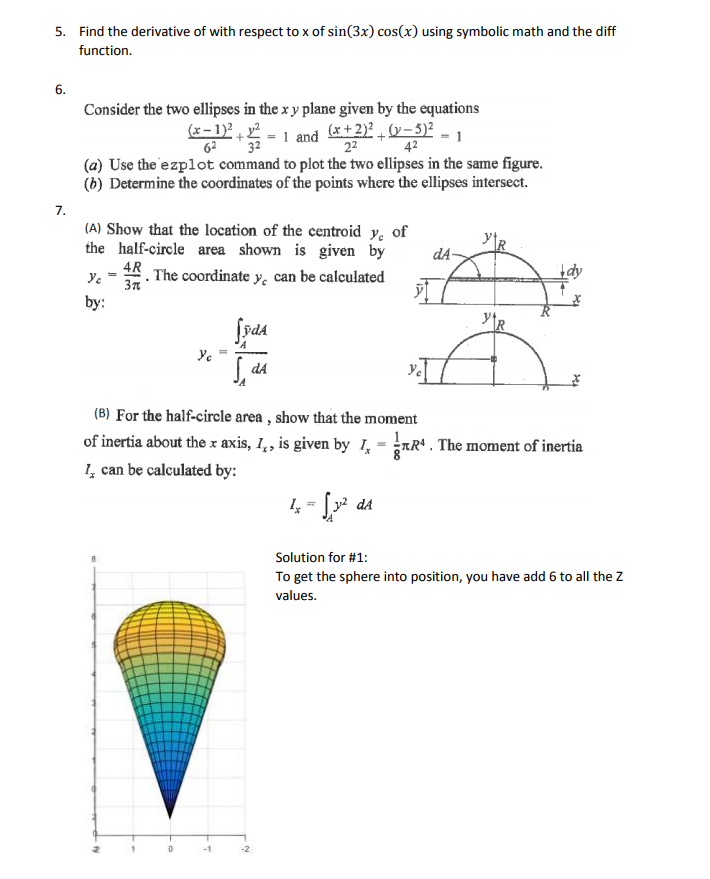
Chapter 10 and 11 Homeworlk Submit these seven problems in one script. 1. Make a 3D plot of an ice cream cone. The cone portion is 6 inches tall with a 3-inch diameter base. The ice cream top is a hemisphere with a diameter of 3 inches. A parametric equation for the cone is: x = r cos() y= r sin() z= 4r with 0 2 and 0 r 1.5 A parametric equation for the sphere is z=rcos(p) x=rcos(8)sin(p) y= rsin()sin() with 0 2 and 0 2. An elliptical staircase that decreases can be modeled by the parametric equations ht 20 where r , a and 20 bcos()2+[asin()12 ox(m) -10 -20 b are the semimajor and semiminor axes of the ellipse, h is the staircase height, and n is the number of revolutions that the staircase makes. Make a 3-D plot of the staircase with a = 20 m, b 10 m, h 1 8 m, and n = 3 . (Create a vector 1 for the domain 0 to 2n, and use the plot3 command.) The geometry of a ship hull (Wigley hull) can be modeled by the equation -04 where x, y, and z are the length, width, and height, respectively. Use MAT-1 LAB to make a 3-D figure of the hull as shown. Use B-1.2, L- 4, T= 0.5,-2 x 2,and-0.5 z 0 4. Define x as a symbolic variable and create two symbolic expressions Sl =X2(X-5) + 7(3x-4) S2 = (x + 3)2-8x (a) Use symbolic operations to determine the simplest form of S1 times S2. (b) Use symbolic operations to determine the simplest form of S1 minus S2 (c) Use the subs command to calculate the numerical value of S1 minus S2 when x = 5