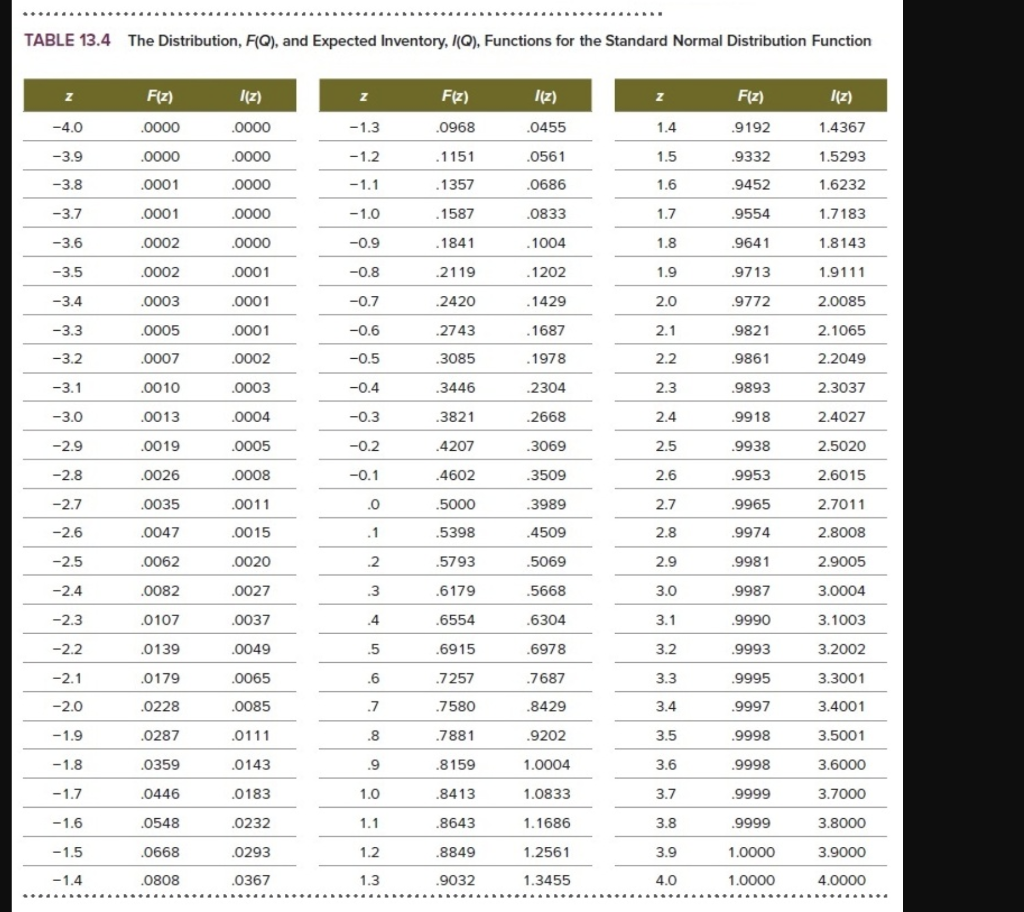
Question: HELP please :) Use Table 13.4 CPG Bagels starts the day with a large production run of bagels. Throughout the morning additional bagels are produced
HELP please :)

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


