Help with part D$.$New angular velocity.

Part A $-$ Linear momentum

Calculate the magnitude of the linear momentum of the disk for the given velocities.

Express your answer to three significant figures in slug$-$foot per second.

View Available Hint$($s$)$

Previous Answers

Correct

Part B $-$ Angular momentum about G

Calculate the magnitude of the angular momentum about the disk's center of gravity, $G,$ for the given dimensions and angular velocity.

Express your answer to three significant figures in slug$-$foot squared per second.

View Available Hint$($s$)$

Correct

Part C $-$ Change in linear momentum

The disk from Part A is now moving in the opposite direction with a velocity of $v_2=18\mathrm{.}0f\frac{t}{s}$ and an angular velocity of ${}_2=12\mathrm{.}0ra\frac{d}{s}$ in the direction shown in $($Figure $2).$ What is the change in the disk's linear momentum?

Express your answer to three significant figures in slug$-$foot per second.

View Available Hint$($s$)$

$L=-223$i slug $*f\frac{t}{s}$

Part D $-$ New angular velocity

The disk from Part C $,$ which had an angular velocity of ${}_2=12\mathrm{.}0$kra$\frac{d}{s},$ has undergone a change in angular momentum, $H_{IC}=-14\mathrm{.}7k$ slug $*f\frac{t^2}{s}.$ Calculate the new angular velocity of the disk.

Express your answer to three significant figures and include the appropriate units.

View Available Hint$($s$)$

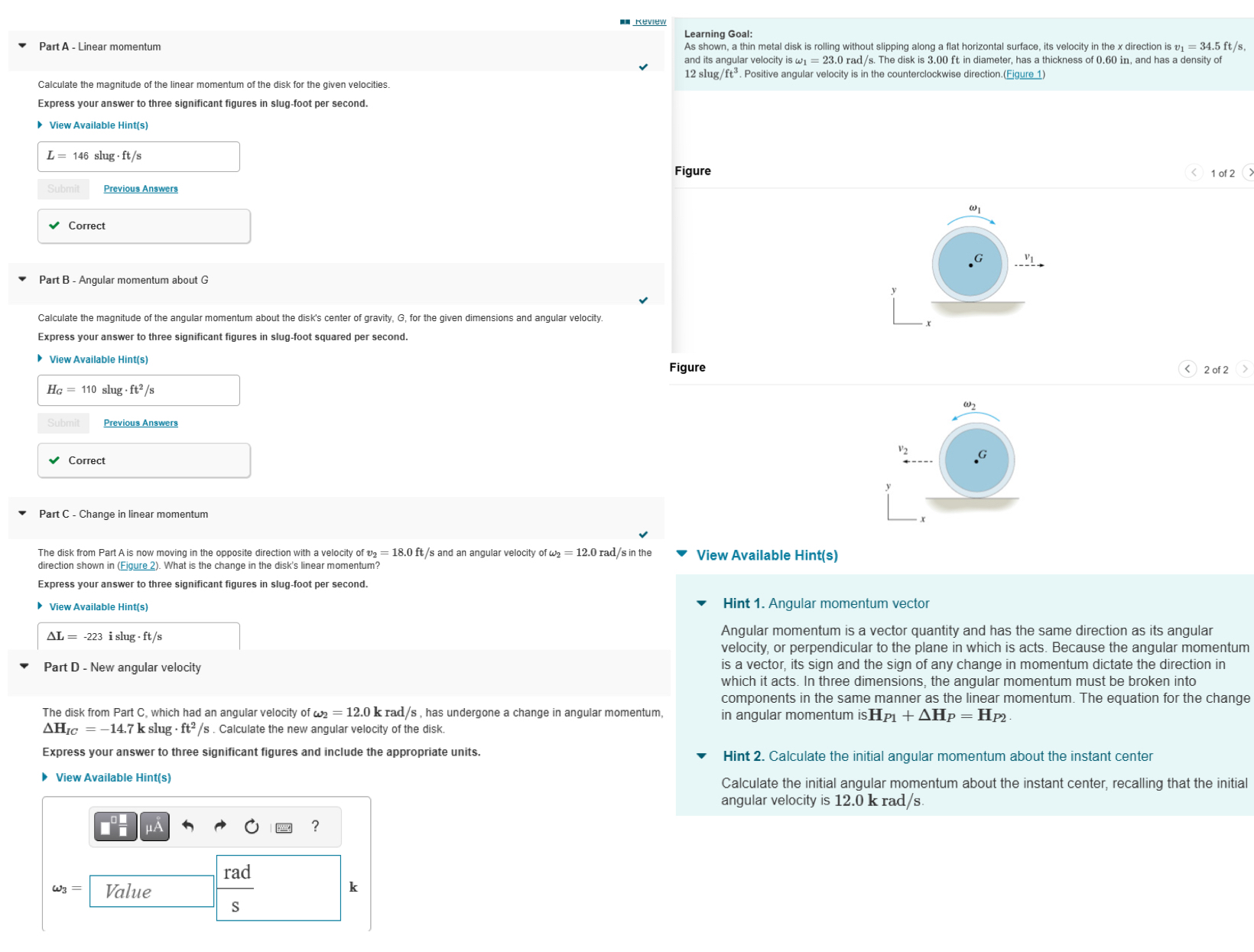
Learning Goal:

As shown, a thin metal disk is rolling without slipping along a flat horizontal surface, its velocity in the $x$ direction is $v_1=34\mathrm{.}5f\frac{t}{s},$ and its angular velocity is ${}_1=23\mathrm{.}0ra\frac{d}{s}.$ The disk is $3\mathrm{.}00$ ft in diameter, has a thickness of $0\mathrm{.}60$ in $,$ and has a density of $12$ slug $\frac{?}{f{t}^3}.$ Positive angular velocity is in the counterclockwise direction.$($Eigure $1)$

Figure

$1$ of $2$

Figure

$2$ of $2$

View Available Hint$($s$)$

Hint $1.$ Angular momentum vector

Angular momentum is a vector quantity and has the same direction as its angular velocity, or perpendicular to the plane in which is acts. Because the angular momentum is a vector, its sign and the sign of any change in momentum dictate the direction in which it acts. In three dimensions, the angular momentum must be broken into components in the same manner as the linear momentum. The equation for the change in angular momentum is $H_{P1}+H_P=H_{P2}.$

Hint $2.$ Calculate the initial angular momentum about the instant center

Calculate the initial angular momentum about the instant center, recalling that the initial angular velocity is $12\mathrm{.}0$kra$\frac{d}{s}.$