Help with the linear programming questions below

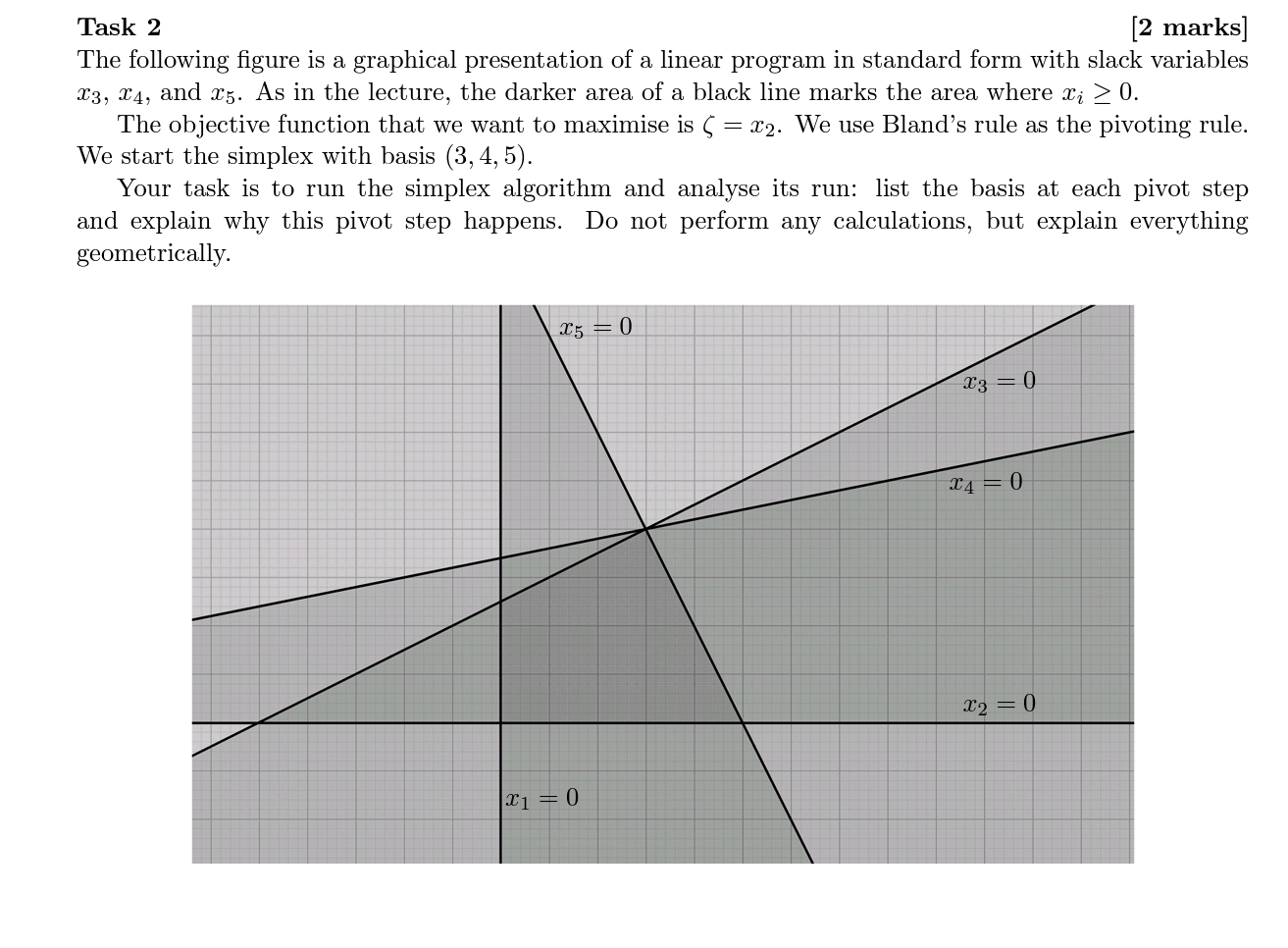
Task 1 [2 marks] A manufacturer has two machines that each can produce two different products, product A and prod uct B. Product A can be sold for if 1000 per metric ton. Product B can be sold for 800 per metric ton. 0 Machine X can run for 40 hours per week. It takes 40 minutes for machine X to produce one metric ton of product A. It takes 30 minutes for machine X to produce one metric ton of product B. 0 Machine Y can run for 35 hours per week. It takes 35 minutes for machine Y to produce one metric ton of product A. It takes 25 minutes for machine Y to produce one metric ton of product B. The manufacturer wants to maximise the sales revenue for one week. (a) Set up the corresponding linear program in standard form. (b) Introduce slack variables and nd an initial feasible primal dictionary to run the primal simplex algorithm (do not actually run the simplex algorithm). Task 2 [2 marks] The following gure is a graphical presentation of a linear program in standard form with slack variables 323, 2:4, and 3:5. As in the lecture, the darker area of a black line marks the area where 3:3- 2 0. The objective function that we want to maximise is C : 332. We use Bland's rule as the pivoting rule. We start the simplex with basis (3, 4, 5). Your task is to run the simplex algorithm and analyse its run: list the basis at each pivot step and explain why this pivot step happens. Do not perform any calculations, but explain everything geometrically