Question: Help with these questions. 10. Let the random variable Y have distribution function G where Buya-le-By G(x) = $(0) + y(0) r(a) dy. The Beekman-Bowers'
Help with these questions.


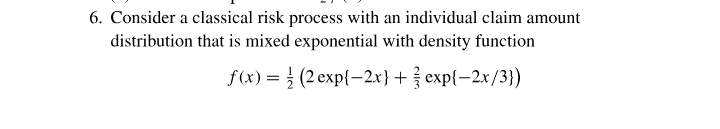
![o and B are chosen such that E[Y' ] = E[L'] for](https://s3.amazonaws.com/si.experts.images/answers/2024/07/668a34a28f239_474668a34a262c6b.jpg)
10. Let the random variable Y have distribution function G where Buya-le-By G(x) = $(0) + y(0) r(a) dy. The Beekman-Bowers' approximation uses G(u) as an approximation to ((u), where the parameters o and B are chosen such that E[Y' ] = E[L'] for r = 1, 2. (a) Show that when F(x) = 1 -e-#x x 2 0, G(u) = $(u). (b) Repeat question 6(c), but now use the Beekman-Bowers' approximation to v (u). 11. Let the individual claim amount distribution be exponential with mean 1/o, and let c = (1 + 0)2/o. Use formula (7.19) to show that $(4) = 1- 1+0 exp {-a0/(1 +0) ).for x > 0. The premium for this risk is calculated with a loading factor of 10%. (a) Find the adjustment coefficient. (b) Use the method of Laplace transforms to find an expression for D (u). (c) Find De Vylder's approximation to v(u), and calculate exact and approximate values of vr(u) for u = 0, 10, 20, ..., 50. Comment on the quality of the approximation. 7. Cramer's asymptotic formula is (u) ~ Ce-Ru where R is the adjustment coefficient and c/2 - ml C = E[XeRX] - c/X (a) Show that when F(x) = 1 -e-"*, x 2 0, the asymptotic formula is exact. (b) Repeat question 6(c), but now use Ce-" as an approximation to Vr (u ). 8. (a) Assuming that the required moments exist, show that EL1= mr+1 (r + 1 )mi (b) Find expressions for E[L] and E[L'] in terms of 0 and mx, k = 1, 2, 3, when c = (1 + 0)Am]. 9. Tijms' approximation to y(u) is Ce-Ru + Ae-Su where C and R are as in Cramer's asymptotic formula, A is such that the approximation gives the exact value of v(0), and S is such that J. "(urdu = ( Ce- RW + Ae- Su ) du. (7.29) (a) What is the rationale underlying identity (7.29)? (b) Let the individual claim amount distribution be f (x) = ze-*/2+ hexthe-2x for x > 0, and let the premium loading factor be 5%. Calculate Tijms' approximation to v (20).6. Consider a classical risk process with an individual claim amount distribution that is mixed exponential with density function f(x) = = (2 exp(-2x] + { exp(-2x/3])The risk free rate is 10% and the expected return on the market portfolio is 15%. The expected returns for 4 securities are listed below together with their expected betas SECURITY EXPECTED RETURN EXPECTED BETA 17.0% 1.3 B 14.5% 0.8 C 15.5% 1.1 D 18.0% 1.7 REQUIRED: a. On the basis of these expectations, which securities are overvalued? Which are undervalued? b. If the risk-free rate were to rise to 12% and the expected return on the market portfolio rose to 16%, which securities would be overvalued? which would be under-valued? (Assume the expected returns and the betas remain the same)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


