Help with these questions. Provide clear solutions.

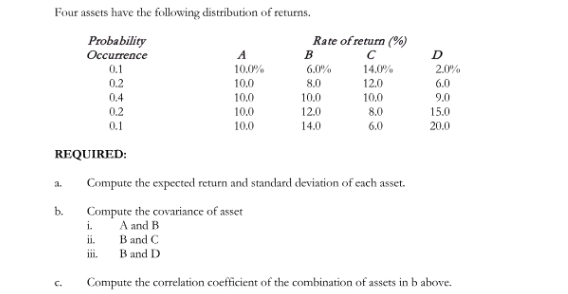
1. Let ,(u, b) denote the probability of ultimate ruin from initial surplus u when there is a reflecting barrier at b 2 u (so that when the surplus process reaches level b, it remains there until a claim occurs). Show that 5, (b, b) = / 5, (b - x, b) f (x ) dx + 1 - F(b) and use the fact that 5, (u, b) 2 5,(b, b) to show that &, (u, b) = 1 for Osusb. 2. An aggregate claims process is a compound Poisson process with Poisson parameter 2, and the individual claim amount density is f(x) = exp(-x} for x > 0. The insurer initially calculates its premium with a loading factor of 0.2. However, when the insurer's surplus reaches level b > u, the loading factor will reduce to 0.1 and will remain at that level thereafter. Calculate the probability of ultimate ruin when u = 10 and b = 20. 3. By conditioning on the time and the amount of the first claim show that " Glu, y) = AG(. y) - 2 { G( - x. y)f()dx - puty f(x)dx. du By integrating this equation over (0, w) show that wty G(w, y) = 2 G(w - x, y) (1 - F(x))dx + - (1 - F(x))dx. w 4. Show that the density of JU(T,)| | T.