help with these two questions please

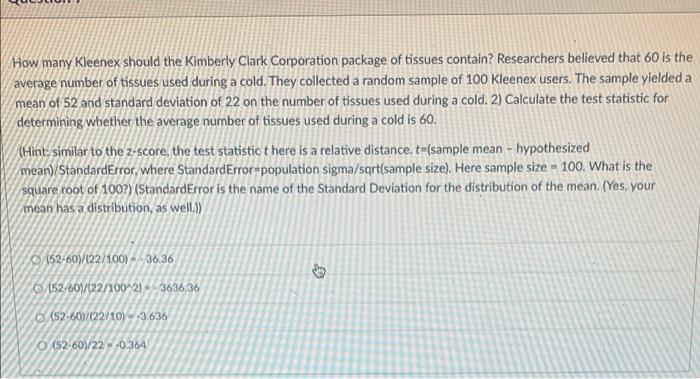
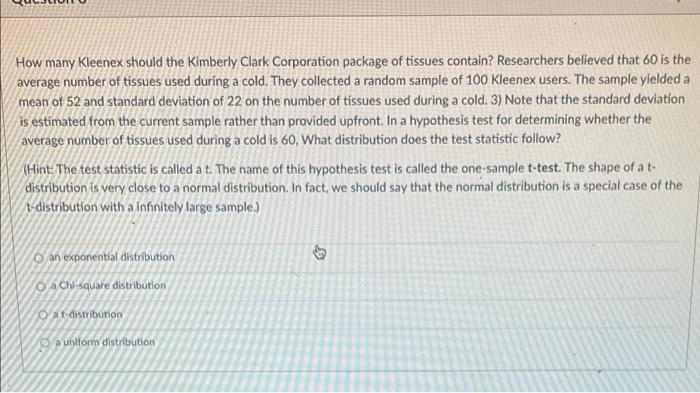
How many Kleenex should the Kimberly Clark Corporation package of tissues contain? Researchers believed that 60 is the average number of tissues used during a cold. They collected a random sample of 100 Kleenex users. The sample yielded a mean of 52 and standard deviation of 22 on the number of tissues used during a cold. 2) Calculate the test statistic for determining whether the average number of tissues used during a cold is 60. (Hint: similar to the 2-score, the test statistic there is a relative distance.te(sample mean - hypothesized mean)/StandardError, where Standard Error-population sigma/sqrt(sample size). Here sample size = 100. What is the square root of 100?) (StandardError is the name of the Standard Deviation for the distribution of the mean. (Yes, your mean has a distribution, as well.) (52-60)/(22/100) -36.36 (52-60)/(22/100-2) -3636.36 (52-60)/122/10) -3.636 (52-60)/22.-6.364 How many Kleenex should the Kimberly Clark Corporation package of tissues contain? Researchers believed that 60 is the average number of tissues used during a cold. They collected a random sample of 100 Kleenex users. The sample yielded a mean of 52 and standard deviation of 22 on the number of tissues used during a cold. 3) Note that the standard deviation is estimated from the current sample rather than provided upfront. In a hypothesis test for determining whether the average number of tissues used during a cold is 60, What distribution does the test statistic follow? (Hint: The test statistic is called a t. The name of this hypothesis test is called the one-sample t-test. The shape of at: distribution is very close to a normal distribution. In fact, we should say that the normal distribution is a special case of the t-distribution with a infinitely large sample.) an exponential distribution Chi-square distribution O at distribution a uniform distribution