here are 9 questions on derivative applications i need help with

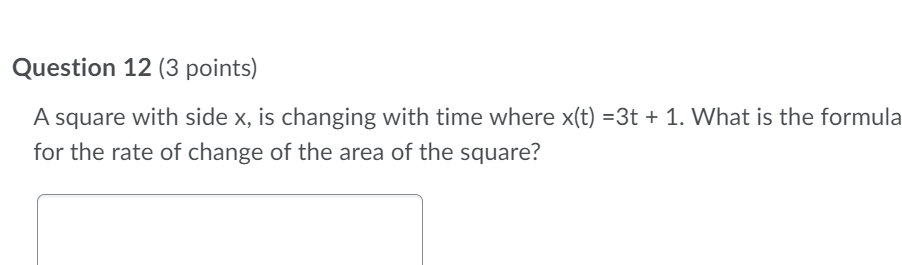
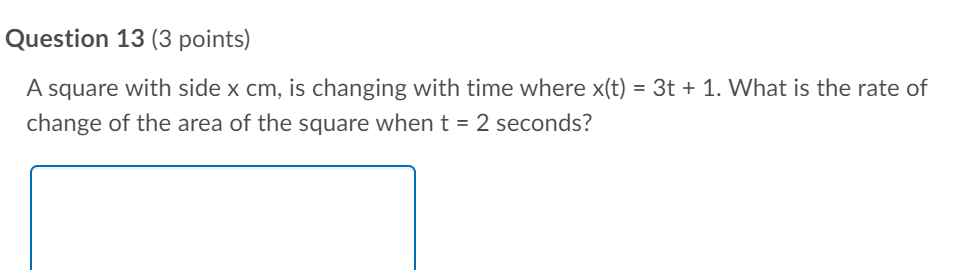
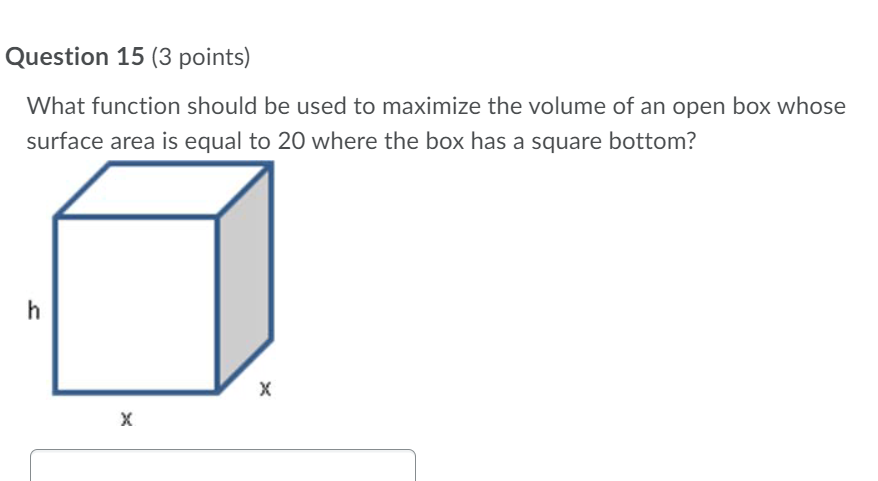
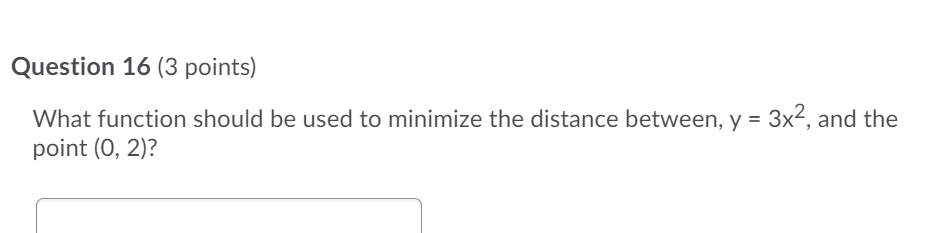
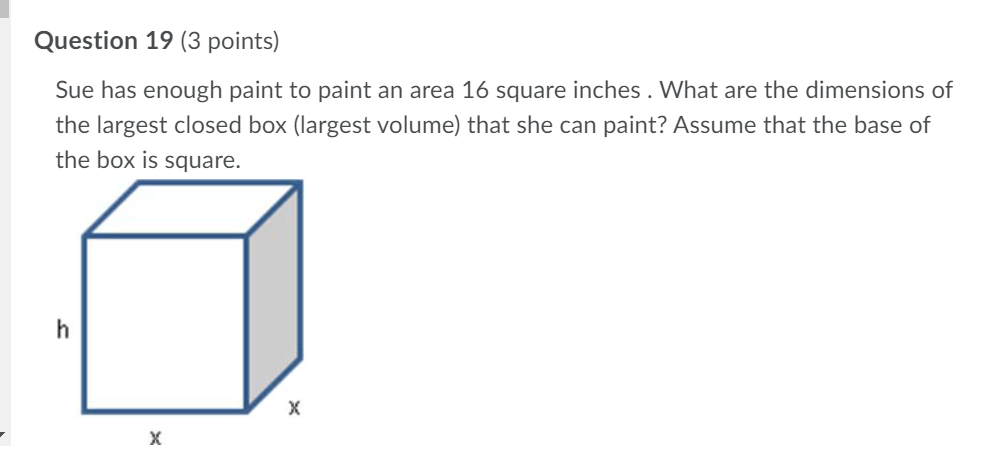
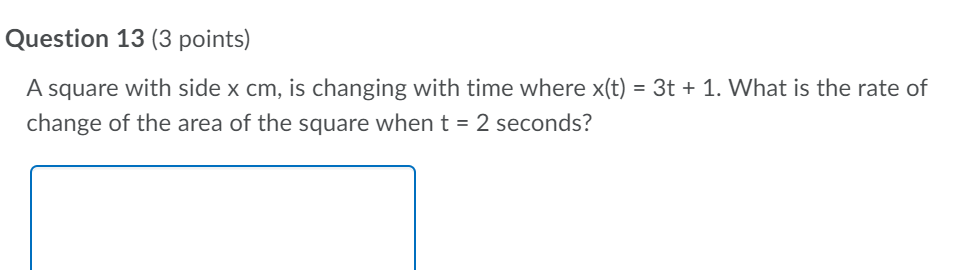
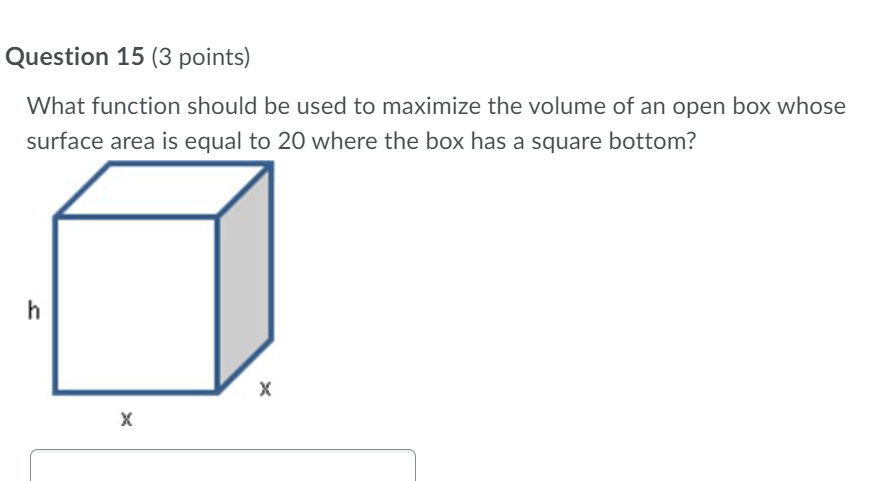
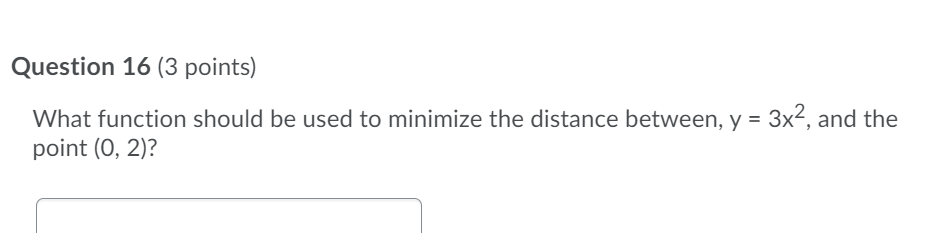
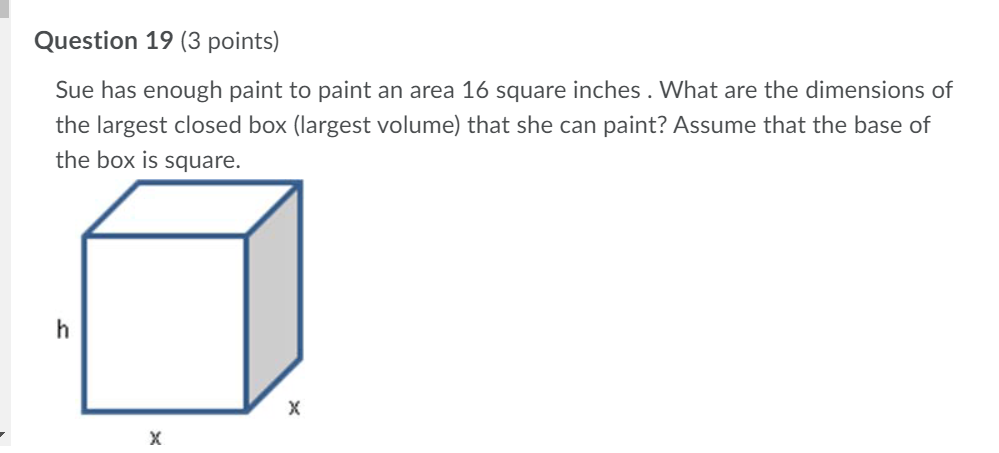
Question 12 (3 points) A square with side x, is changing with time where x(t) =3t + 1. What is the formula for the rate of change of the area of the square? Question 13 (3 points) A square with side x cm, is changing with time where x(t) = 3t + 1. What is the rate of change of the area of the square when t = 2 seconds? Question 14 (3 points) A triangle with constant base b and height h is changing with time where h(t) = 3t + 1. What is the rate of change of the area of the triangle when t = 1?Question 15 {3 points) What function should be used to maximize the volume of an open box whose surface area is equal to 20 where the box has a square bottom? Question 16 {3 points) What function should be used to minimize the distance between, y = 3x2, and the point (0, 2)? i i Question 17 {3 points) What point on the function, y = 3x2 is the closest to {0, 1)? Question 18 (3 points) What value of x maximizes the volume of an open box with a square bottom, where the surface area of the box is equal to 20? Question 19 (3 points) Sue has enough paint to paint an area 16 square inches . What are the dimensions of the largest closed box (largest volume] that she can paint? Assume that the base of the box is square. | Question 20 (3 points) An object is traveling along a path described by 1/: ix + 3 . Where along that path will the object be the closest to the point (2, 0)